Question

已知：AC与BD相交于点O，且OB=OC，OA=OD．求证：△ABC≌△DCB．

Answer 1

考点：全等三角形的判定

专题：证明题

分析：由条件可证明△AOB≌△DOC，可得到AB=CD，∠BAC=∠BDC，且AC=BD，则可证明△ABC≌△DCB．

解答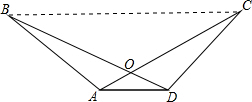：证明：连接BC，
在△AOB和△DOC中，

AO=DO ∠AOB=∠DOC BO=CO

，
∴△AOB≌△DOC（SAS），
∴AB=CD，∠BAC=∠BDC，
∵OB=OC，OA=OD，
∴BD=AC，
在△ABC和△DCB中，

AB=CD ∠BAC=∠BDC AC=BD

，
∴△ABC≌△DCB（SAS）．

点评：本题主要考查全等三角形的判定和性质，掌握利用全等三角形可以为证明三角形全等寻找所需要的条件是解题的关键．