题目内容
如图，在?ABCD中，E是AD的中点，CE交对角线BD于O点，则| EO |
| OC |
考点：平行四边形的性质,相似三角形的判定与性质
专题：
分析：首先利用平行四边形的性质得出AD∥BC，AD=BC，即可得出△DEO∽△BCO，再利用相似三角形的性质得出答案．
解答：解：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∴△DEO∽△BCO，
∴
=
，
∵E是AD的中点，
∴
=
=
．
故答案为：
．
∴AD∥BC，AD=BC，
∴△DEO∽△BCO，
∴
| EO |
| CO |
| DE |
| BC |
∵E是AD的中点，
∴
| EO |
| CO |
| DE |
| BC |
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：此题主要考查了平行四边形的性质以及相似三角形的判定与性质，得出△DEO∽△BCO是解题关键．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
已知一次函数y=（1+2m）x-3中，函数值y随自变量x的增大而增大，那么m的取值范围是（ ）
A、m＞
| ||
B、m＜
| ||
C、m＜-
| ||
D、m＞-
|
已知x=-1是一元一次方程ax=2-x的解，则a的值是（ ）
| A、-3 | B、3 | C、1 | D、-1 |
若关于x的一元二次方程x2+px+q=0的两根分别为x1=2，x2=1，则p、q的值分别是（ ）
| A、3、2 | B、-2、3 |
| C、-3、2 | D、2、3 |
已知等腰△ABC的边长为3、5，则腰AC的长可能为（ ）
| A、5 | B、5或3 | C、3 | D、2 |
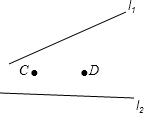如图，一个人从C点骑马出发到D点，但他必须先到河岸边l1的P1点去让马饮水，然后再到河岸边l2的P2点去，再次让马饮水，最后骑马到D点，他应如何选择饮水点P1，P2．才能使所走的路程CP1+P1P2+P2D最短？