题目内容
已知:如图,在Rt△ABC中,∠ C=90°,BD平分∠ABC,交AC于点D,经过B、D两点的⊙O交AB 于点E,交BC于点F, EB为⊙O的直径.

(1)求证:AC是⊙O的切线;
(2)当BC=2,cos∠ABC= 时,求⊙O的半径.
时,求⊙O的半径.
(1)证明见试题解析;(2) .
.
【解析】
试题分析:(1)连结OD,可证得OD∥BC,得到∠ADO=∠C=90°,从而得出结论;
(2)由cos∠ABC= ,得到AB=6,由△AOD∽△ABC,得到圆的半径.
,得到AB=6,由△AOD∽△ABC,得到圆的半径.
试题解析:(1)证明:如图,连结OD,∴OD=OB,∴∠1=∠2,∵BD平分∠ABC,∴∠1=∠3,∴∠2=∠3.∴OD∥BC,∴∠ADO=∠C=90°,∴OD⊥AC,∵OD是⊙O的半径,∴ AC是⊙O的切线;

(2)在Rt△ACB中,∠C=90°,BC=2 , cos∠ABC  ,∴
,∴  .设⊙O的半径为
.设⊙O的半径为 ,则AO=6-r,∵OD∥BC,∴△AOD∽△ABC,∴
,则AO=6-r,∵OD∥BC,∴△AOD∽△ABC,∴  ,∴
,∴  ,解得
,解得  ,∴ ⊙O的半径为
,∴ ⊙O的半径为 .
.
考点:1.切线的判定;2.相似三角形的判定与性质.

练习册系列答案
相关题目
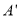 ,
,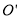 .设∠ABP =α.
.设∠ABP =α.
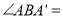 °;
°;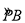 上时,求出
上时,求出 的度数.
的度数. 与x轴,y轴分别交于点A,B,抛物线
与x轴,y轴分别交于点A,B,抛物线 过点A和点C (4,0) .
过点A和点C (4,0) .

 B.
B. C.
C. D.
D.
 的解为( )
的解为( )
 ,
,

 ,
, 的图象与反比例函数
的图象与反比例函数 的图象交于A(-1,4),B(2,m)两点.
的图象交于A(-1,4),B(2,m)两点.
 的解集.
的解集. 的顶点坐标是 .
的顶点坐标是 . ,以
,以 、
、 为边向
为边向 和等边
和等边 ,连接
,连接 ,
, .请画出图形,并证明:
.请画出图形,并证明: ; (4分)
; (4分) 和
和 .连接
.连接 ,
, .
. 、
、 的距离,已经测得
的距离,已经测得 ,
, ,
, 米,
米, 米,
米, ,求
,求 的长.
的长.