题目内容
5．二次函数y=ax2+bx+c的变量x与变量y的部分对应值如下表：| x | … | -3 | -2 | -1 | 0 | 1 | 5 | … |
| y | … | 7 | 0 | -5 | -8 | -9 | 7 | … |
（2）写出抛物线顶点坐标和对称轴．
分析 （1）把（-2，0），（-1，-5），（0，-8）代入y=ax2+bx+c中，根据待定系数法即可求得；
（2）把解析式化成顶点式即可求得．
解答 解：（1）把（-2，0），（-1，-5），（0，-8）代入y=ax2+bx+c得
$\left\{\begin{array}{l}{4a-2b+c=0}\\{a-b+c=-5}\\{c=-8}\end{array}\right.$，解得$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=-8}\end{array}\right.$，
∴二次函数的解析式为y=x2-2x-8；
（2）∵y=x2-2x-8=（x-1）2-9，
∴抛物线顶点坐标为（1，-9），对称轴为直线x=1．
点评 本题考查了待定系数法求二次函数的解析式以及二次函数的顶点坐标和对称轴，熟练掌握待定系数法是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
13．
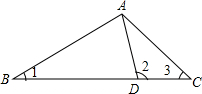如图，在△ABC中，D是BC上一点，∠1+∠2+∠3=180°，$\frac{CD}{BD}$=$\frac{1}{3}$，则$\frac{AD}{AB}$=（ ）
如图，在△ABC中，D是BC上一点，∠1+∠2+∠3=180°，$\frac{CD}{BD}$=$\frac{1}{3}$，则$\frac{AD}{AB}$=（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{3}}{3}$ |
17．
如图，AD平分∠BAC，DE⊥AB于点E，S△ACD=3，DE=2，则AC长是（ ）
如图，AD平分∠BAC，DE⊥AB于点E，S△ACD=3，DE=2，则AC长是（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
一个正方体六个面分别标有字母A、B、C、D、E、F，其展开如图所示，已知：A=x2-2xy、B=A-C，C=3xy+y2，若该正方体相对两个面上的多项式的和相等，试用x、y的代数式表示多项式D，并求当x=-1，y=-2时，多项式D的值．