题目内容
18. 已知:如图,ABCD为正方形,边长为a,以B为圆心,以BA为半径画弧,则阴影部分面积为( )
已知:如图,ABCD为正方形,边长为a,以B为圆心,以BA为半径画弧,则阴影部分面积为( )| A. | (1-π)a2 | B. | 1-π | C. | $\frac{4-π}{4}$ | D. | $\frac{4-π}{4}$a2 |
分析 S阴影面积=S正方形-S扇形BAC,然后根据扇形和正方形的面积公式进行计算即可.
解答 解:∵ABCD是正方形,边长为a,
∴S阴影面积=S正方形-S扇形BAC=a2-$\frac{90π{a}^{2}}{360}$=$\frac{4-π}{4}$a2.
故选D.
点评 本题考查了扇形的面积公式:S=$\frac{nπ{r}^{2}}{360}$,其中n为扇形的圆心角的度数,R为圆的半径),或S=$\frac{1}{2}$lR,l为扇形的弧长,R为半径.也考查了正方形的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.在3.14,-$\sqrt{2}$,$\root{3}{9}$,π,0.2020020002…五个数中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8. 如图,在△ABC中,∠ACB=120°,AC=AE,BC=BD,则∠DCE的度数为( )
如图,在△ABC中,∠ACB=120°,AC=AE,BC=BD,则∠DCE的度数为( )
 如图,在△ABC中,∠ACB=120°,AC=AE,BC=BD,则∠DCE的度数为( )
如图,在△ABC中,∠ACB=120°,AC=AE,BC=BD,则∠DCE的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
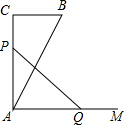 如图,有一Rt△ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P点在AC上,Q点在过A点且垂直于AC的射线AM上运动.当△ABC和△APQ全等时,点Q到点A的距离为10cm或5cm.
如图,有一Rt△ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P点在AC上,Q点在过A点且垂直于AC的射线AM上运动.当△ABC和△APQ全等时,点Q到点A的距离为10cm或5cm. 如图,有一个英语单词,四个字母都关于直线l对称,请写出这个单词BOOK.
如图,有一个英语单词,四个字母都关于直线l对称,请写出这个单词BOOK.