题目内容
已知△ABC的三边分别是a，b，c且a，b满足
+（b-4）2=0，求c的取值范围．
| a-3 |
考点：非负数的性质：算术平方根,非负数的性质：偶次方,三角形三边关系
专题：
分析：根据非负数的性质列式求出a、b，再根据三角形的任意两边之和大于第三边，三角形的任意两边之差小于第三边求解即可．
解答：解：由题意得，a-3=0，b-4=0，
解得a=3，b=4，
∵3+4=7，4-3=1，
∴1＜c＜7．
解得a=3，b=4，
∵3+4=7，4-3=1，
∴1＜c＜7．
点评：本题考查了三角形的三边关系，非负数的性质：几个非负数的和为0时，这几个非负数都为0．
练习册系列答案
名校课堂系列答案
相关题目
已知|a|=3，b2=4，且ab＞0，则a+2b=（ ）
| A、7 | B、-7 |
| C、7或-7 | D、1或-1 |
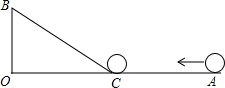如图，∠AOB=90°，OA=90cm，OB=30cm，一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O，机器人立即从点B出发，沿直线立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球，如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是多少？在平面直角坐标系中，点A坐标为（1，3），将点A向左平移2个单位长度，得到点A′，则点A′的坐标为（ ）
| A、（3，3） |
| B、（-1，3） |
| C、（0，3） |
| D、（3，-1） |