题目内容
16.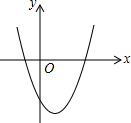 二次函数y=x2-2x-3的图象如图所示,若线段AB在x轴上,且AB为2$\sqrt{3}$个单位长度,以AB为边作等边△ABC,使点C落在该函数y轴右侧的图象上,则点C的坐标为(1+$\sqrt{7}$,3)或(2,-3).
二次函数y=x2-2x-3的图象如图所示,若线段AB在x轴上,且AB为2$\sqrt{3}$个单位长度,以AB为边作等边△ABC,使点C落在该函数y轴右侧的图象上,则点C的坐标为(1+$\sqrt{7}$,3)或(2,-3).
分析 △ABC是等边三角形,且边长为2$\sqrt{3}$,所以该等边三角形的高为3,又点C在二次函数上,所以令y=±3代入解析式中,分别求出x的值.由因为使点C落在该函数y轴右侧的图象上,所以x>0.
解答 解:∵△ABC是等边三角形,且AB=2$\sqrt{3}$,
∴AB边上的高为3,
又∵点C在二次函数图象上,
∴C的纵坐标为±3,
令y=±3代入y=x2-2x-3,
∴x=1$±\sqrt{7}$或0或2
∵使点C落在该函数y轴右侧的图象上,
∴x>0,
∴x=1+$\sqrt{7}$或x=2
∴C(1+$\sqrt{7}$,3)或(2,-3)
故答案为:(1+$\sqrt{7}$,3)或(2,-3)
点评 本题考查二次函数的图象性质,涉及等边三角形的性质,分类讨论的思想等知识,题目比较综合,解决问题的关键是根据题意得出C的纵坐标为±3.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
6. 长方体的主视图与左视图如图所示(单位:cm),则其俯视图的面积是( )
长方体的主视图与左视图如图所示(单位:cm),则其俯视图的面积是( )
 长方体的主视图与左视图如图所示(单位:cm),则其俯视图的面积是( )
长方体的主视图与左视图如图所示(单位:cm),则其俯视图的面积是( )| A. | 4cm2 | B. | 6cm2 | C. | 8cm2 | D. | 12cm2 |
7.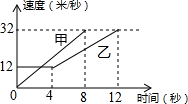 如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
 如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )| A. | 乙前4秒行驶的路程为48米 | |
| B. | 在0到8秒内甲的速度每秒增加4米/秒 | |
| C. | 两车到第3秒时行驶的路程相等 | |
| D. | 在4至8秒内甲的速度都大于乙的速度 |
4.若x2-3y-5=0,则6y-2x2-6的值为( )
| A. | 4 | B. | -4 | C. | 16 | D. | -16 |
6.一元二次方程x2-x-1=0的根的情况为( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
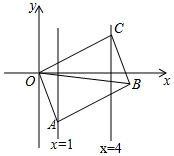 如图,已知?OABC的顶点A、C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为5.
如图,已知?OABC的顶点A、C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为5. 下列选项中,不是如图所示几何体的主视图、左视图、俯视图之一的是( )
下列选项中,不是如图所示几何体的主视图、左视图、俯视图之一的是( )



 如图,利用尺规,在△ABC的边AC上方作∠CAE=∠ACB,在射线AE上截取AD=BC,连接CD,并证明:CD∥AB(尺规作图要求保留作图痕迹,不写作法)
如图,利用尺规,在△ABC的边AC上方作∠CAE=∠ACB,在射线AE上截取AD=BC,连接CD,并证明:CD∥AB(尺规作图要求保留作图痕迹,不写作法) 如图所示,四边形ABCD的对角线相交于点O,若AB∥CD,请添加一个条件AD∥BC(写一个即可),使四边形ABCD是平行四边形.
如图所示,四边形ABCD的对角线相交于点O,若AB∥CD,请添加一个条件AD∥BC(写一个即可),使四边形ABCD是平行四边形.