题目内容
如图,点G、E、A、B在一条直线上,Rt△EFG从如图所示是位置出发,沿直线AB向右匀速运动,当点G与B重合时停止运动.设△EFG与矩形ABCD重合部分的面积为S,运动时间为t,则S与t的图象大致是
A. B.
B. C.
C. D.
D.
D
解析试题分析:设GE=a,EF=b,AE=m,AB=c,Rt△EFG向右匀速运动的速度为1,
当E点在点A左侧时,S=0。
当点G在点A左侧,点E在点A右侧时,如答图1,
AE=t﹣m,GA=a﹣(t﹣m)=a+m﹣t,
∵PA∥EF,∴△GAP∽△GEF。
∴ ,即
,即 。∴
。∴ 。
。
∴ 。
。
∴S是t的二次函数,且二次项系数为负数,所以抛物线开口向下。
当点G在点A右侧,点E在点B左侧时,S= ab。
ab。
当点G在点B左侧,点E在点B右侧时,如答图2,
GB=a+m+c﹣t,
∵PA∥EF,∴△GBP∽△GEF。
∴ ,即
,即 。∴
。∴ 。
。
∴ 。
。
∴S是t的二次函数,且二次项系数为,正数,所以抛物线开口向上。
综上所述,S与t的图象分为四段,第一段为x轴上的一条线段,第二段为开口向下的抛物线的一部分,第三段为与x轴平行的线段,第四段为开口先上的抛物线的一部分。
故选D。

如图所示,△ABC∽△DEF 其相似比为K , 则一次函数 的图像与两坐标轴围成的三角形面积是( )
的图像与两坐标轴围成的三角形面积是( )
| A.0.5 | B.4 | C.2 | D. 1 |
如图,直角梯形ABCD中,AB∥CD,∠C=90°,∠BDA=90°,AB=a,BD=b,CD=c,BC=d,AD=e,则下列等式成立的是
| A.b2=ac | B.b2=ce | C.be=ac | D.bd=ae |
下列四个命题中,属于真命题的是
A.若 ,则a=m ,则a=m |
| B.若a>b,则am>bm |
| C.两个等腰三角形必定相似 |
| D.位似图形一定是相似图形 |
如图,平行四边形ABCD中,AB∶BC=3∶2,∠DAB=60°,E在AB上,且AE∶EB=1∶2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP∶DQ等于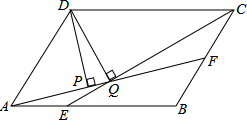
| A.3∶4 | B. ∶ ∶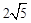 | C. ∶ ∶ | D. ∶ ∶ |
如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则 的值为【 】
的值为【 】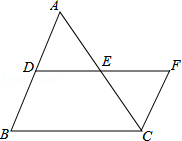
| A.1:3 | B.2:3 | C.1:4 | D.2:5 |
如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3、4及x,那么x的值
| A.只有1个 | B.可以有2个 | C.可以有3个 | D.有无数个 |
 在横杆
在横杆 的正上方,
的正上方, ,
, ,
, ,点
,点 的距离是3m,则点
的距离是3m,则点
 m
m


