题目内容
 如图,在正方形ABCD内作一个等边△BEC,连接AE、DE,则∠BEA=
如图,在正方形ABCD内作一个等边△BEC,连接AE、DE,则∠BEA=考点:正方形的性质,等边三角形的性质
专题:
分析:正方形ABCD中,BC=AB,等边△BCE中,BE=AB,即可得AB=BE,因为∠ABE=30°,利用三角形的内角和为180°即可求出∠BEA的度数.
解答:解:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∵△BEC是等边三角形,
∴BC=BE=CE,∠EBC=60°,
∴AB=BE,∠ABE=30°,
∴∠BEA=
=75°,
故答案为:75°.
∴AB=BC,∠ABC=90°,
∵△BEC是等边三角形,
∴BC=BE=CE,∠EBC=60°,
∴AB=BE,∠ABE=30°,
∴∠BEA=
| 180°-30° |
| 2 |
故答案为:75°.
点评:本题考查了正方形各边长相等、各内角为直角的性质,考查了等边三角形各内角为60°、各边长相等的性质,考查了三角形内角和为180°的性质,本题中求AB=BE是解题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 如图,在矩形ABCD中,点E在AD上,且EC平分∠BED.
如图,在矩形ABCD中,点E在AD上,且EC平分∠BED.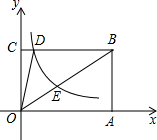 如图,已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线y=
如图,已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线y= 如图,△ABC的周长为28cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连接AD.若AE=4cm,则△ABD的周长是
如图,△ABC的周长为28cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连接AD.若AE=4cm,则△ABD的周长是