题目内容
9. 已知AD⊥BC,∠B=45°,∠C=30°.
已知AD⊥BC,∠B=45°,∠C=30°.(1)当AD=2,求BC的长度;
(2)若BC=4,求AD的长度.
分析 (1)由已知条件得到∠ADB=∠ADC=90.在Rt△ACD中,根据tanC=$\frac{AD}{CD}$=$\frac{2}{CD}$=tan30°=$\frac{\sqrt{3}}{3}$,求得CD=2$\sqrt{3}$,在Rt△ABD中,根据tanB=$\frac{AD}{BD}$=$\frac{2}{BD}$=tan45°=1,求得BD=2,于是得到BC=BD+CD=2$\sqrt{3}+2$;
(2)根据已知条件得到∠ADB=∠ADC=90.在Rt△ACD中,根据tanC=$\frac{AD}{CD}$=tan30°=$\frac{\sqrt{3}}{3}$,求得CD=$\sqrt{3}$AD,在Rt△ABD中,根据tanB=$\frac{AD}{BD}$=tan45°=1,求得BD=AD,于是得到BC=BD+CD=$\sqrt{3}$AD+AD=4,即可得到结论.
解答 解:(1)∵AD⊥BC,
∴∠ADB=∠ADC=90.
在Rt△ACD中,
∵tanC=$\frac{AD}{CD}$=$\frac{2}{CD}$=tan30°=$\frac{\sqrt{3}}{3}$,
∴CD=2$\sqrt{3}$,
在Rt△ABD中,
∵tanB=$\frac{AD}{BD}$=$\frac{2}{BD}$=tan45°=1,
∴BD=2,
∴BC=BD+CD=2$\sqrt{3}+2$,
即BC的长为2$\sqrt{3}$+2;
(2))∵AD⊥BC,
∴∠ADB=∠ADC=90.
在Rt△ACD中,
∵tanC=$\frac{AD}{CD}$=tan30°=$\frac{\sqrt{3}}{3}$,
∴CD=$\sqrt{3}$AD,
在Rt△ABD中,
∵tanB=$\frac{AD}{BD}$=tan45°=1,
∴BD=AD,
∴BC=BD+CD=$\sqrt{3}$AD+AD=4,
∴AD=2$\sqrt{3}$-2.
点评 本题考查了解直角三角形,含30°角的直角三角形的性质,等腰直角三角形的性质,解答本题的关键是在直角三角形中利用解直角三角形的知识求出BD、DC的长度.

 名校课堂系列答案
名校课堂系列答案| A. | 36° | B. | 18° | C. | 72° | D. | 54° |
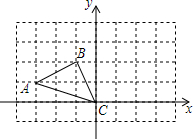 如图所示,在方格纸上建立的平面直角坐标系中:
如图所示,在方格纸上建立的平面直角坐标系中:
 用反证法证明命题“已知D,E分别为△ABC的边AB,AC上的点,BE,CD交于点F,则BE,CD不能互相平分”是真命题.
用反证法证明命题“已知D,E分别为△ABC的边AB,AC上的点,BE,CD交于点F,则BE,CD不能互相平分”是真命题.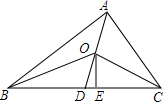 如图,△ABC中,∠ACB>∠ABC,点O是△ABC的内角平分线的交点,AO的延长线交BC于点D,OE⊥BC于点E.
如图,△ABC中,∠ACB>∠ABC,点O是△ABC的内角平分线的交点,AO的延长线交BC于点D,OE⊥BC于点E.