题目内容
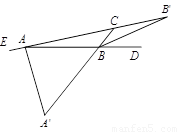
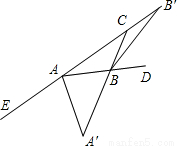
 如图,AA′,BB′分别是∠EAB,∠DBC的平分线.若AA′=BB′=AB,则∠BAE的度数为
如图,AA′,BB′分别是∠EAB,∠DBC的平分线.若AA′=BB′=AB,则∠BAE的度数为
- A.150°
- B.168°
- C.135°
- D.160°
B
分析:从已知条件结合图形,根据等腰三角形的外角和内角的关系以及三角形内角和定理求解.
解答:设∠BAC=x,
∵BB′=AB,
∴∠B′BD=2∠BAC=2x,
又∵BB′是∠DBC的平分线,
∴∠DBC=2∠B′BD=4x,
∵AA′=AB,
∴∠A′=∠A′BA=∠DBC=4x,
∵AA′是∠EAB的平分线,
∴∠A′AB= (180°-x),
(180°-x),
在△AA′B中,根据内角和定理:4x+4x+ (180°-x)=180°,解得x=12°,即∠BAC=12°.
(180°-x)=180°,解得x=12°,即∠BAC=12°.
∴∠BAE=180°-12°=168°.
故选B.
点评:本题考查的是三角形外角的性质及三角形内角和定理,做题时,要综合运用这些知识是十分必要的.
分析:从已知条件结合图形,根据等腰三角形的外角和内角的关系以及三角形内角和定理求解.
解答:设∠BAC=x,
∵BB′=AB,
∴∠B′BD=2∠BAC=2x,
又∵BB′是∠DBC的平分线,
∴∠DBC=2∠B′BD=4x,
∵AA′=AB,
∴∠A′=∠A′BA=∠DBC=4x,
∵AA′是∠EAB的平分线,
∴∠A′AB=
 (180°-x),
(180°-x),在△AA′B中,根据内角和定理:4x+4x+
 (180°-x)=180°,解得x=12°,即∠BAC=12°.
(180°-x)=180°,解得x=12°,即∠BAC=12°.∴∠BAE=180°-12°=168°.
故选B.
点评:本题考查的是三角形外角的性质及三角形内角和定理,做题时,要综合运用这些知识是十分必要的.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,AA′,BB′分别是∠EAB,∠DBC的平分线,若AA′=BB′=AB,则∠BAC的度数为( )
如图,AA′,BB′分别是∠EAB,∠DBC的平分线,若AA′=BB′=AB,则∠BAC的度数为( )| A、25° | B、30° | C、12° | D、18° |
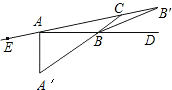 如图,AA′、BB′分别是∠EAB、∠DBC的平分线,若AA′=BB′=AB,则∠BAC的度数为
如图,AA′、BB′分别是∠EAB、∠DBC的平分线,若AA′=BB′=AB,则∠BAC的度数为 如图,AA′,BB′分别是∠EAB,∠DBC的平分线.若AA′=BB′=AB,则∠BAE的度数为( )
如图,AA′,BB′分别是∠EAB,∠DBC的平分线.若AA′=BB′=AB,则∠BAE的度数为( )