题目内容
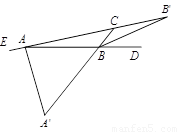
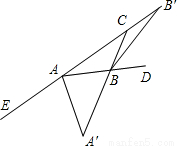
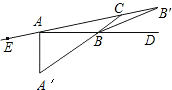 如图,AA′、BB′分别是∠EAB、∠DBC的平分线,若AA′=BB′=AB,则∠BAC的度数为
如图,AA′、BB′分别是∠EAB、∠DBC的平分线,若AA′=BB′=AB,则∠BAC的度数为分析:设∠BAC为x°,根据等腰三角形的性质及三角形外角的性质可得到∠CBD=4x°,再根据角平分线的定义可表示出∠A′AB的度数,再根据三角形内角和定理不难求解.
解答:解:设∠BAC为x°,
∵AB=BB′,
∴∠CAB=∠BB′A,
∴∠B′BD=2x°,
∵BB′是∠DBC的平分线,
∴∠CBD=4x°,
∵AB=AA′,
∴∠AA′B=∠ABA′=∠CBD=4x°,
∵∠A′AB=
(180°-x°),
∴
(180°-x°)+4x°+4x°=180°,
∴x°=12°.
故答案为:12°.
∵AB=BB′,
∴∠CAB=∠BB′A,
∴∠B′BD=2x°,
∵BB′是∠DBC的平分线,
∴∠CBD=4x°,
∵AB=AA′,
∴∠AA′B=∠ABA′=∠CBD=4x°,
∵∠A′AB=
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴x°=12°.
故答案为:12°.
点评:此题主要考查等腰三角形的性质,三角形外角的性质及三角形内角和定理的综合运用.

练习册系列答案
相关题目
 如图,AA′,BB′分别是∠EAB,∠DBC的平分线,若AA′=BB′=AB,则∠BAC的度数为( )
如图,AA′,BB′分别是∠EAB,∠DBC的平分线,若AA′=BB′=AB,则∠BAC的度数为( )| A、25° | B、30° | C、12° | D、18° |
 如图,AA′,BB′分别是∠EAB,∠DBC的平分线.若AA′=BB′=AB,则∠BAE的度数为( )
如图,AA′,BB′分别是∠EAB,∠DBC的平分线.若AA′=BB′=AB,则∠BAE的度数为( )