题目内容
12．在下列各式的括号里，添上适当的项：（1）（a+b+c）（a-b+c）=[a+（b+c）][a-（b-c）]；
（2）（a-b+c）（a+b-c）=[a-（b-c）][a+（b+c）]；
（3）（-a+b+c）（a+b-c）=[b-（a-c）][b+（a-c）]；
（4）（a+b-c-d）（a-b+c-d）=[（a-c ）+（b-d）][（a+c ）-（b+d ）]．
分析 根据括号前是“+”，添括号后，括号里的各项都不改变符号；若括号前是“-”，添括号后，括号里的各项都改变符号，即可得出答案．
解答 解：（1）（a+b+c）（a-b+c）=[a+（b+c）][a-（b-c）]；
（2）（a-b+c）（a+b-c）=[a-（b-c）][a+（b+c）]；
（3）（-a+b+c）（a+b-c）=[b-（a-c）][b+（a-c）]；
（4）（a+b-c-d）（a-b+c-d）=[（a-c）+（b-d）][（a+c）-（b+d）]．
故答案为：（1）（b+c），（b-c）；（2）（b-c），（b+c）；（3）（a-c），（a-c）；（4）-c，-d，+c，+d．
点评 本题考查了添括号，添括号时，若括号前是“+”，添括号后，括号里的各项都不改变符号；若括号前是“-”，添括号后，括号里的各项都改变符号．
练习册系列答案
相关题目
2．13600000=1.36×10a，3590000=3.59×10b，那么（b-a）5=（ ）
| A． | 1 | B． | -1 | C． | 2 | D． | -2 |
3．下列计算结果，正确的是（ ）
| A． | $\sqrt{（-6）^{2}}$=-6 | B． | $\sqrt{2}×\sqrt{5}$=$\sqrt{7}$ | C． | 2+$\sqrt{3}$=$\root{2}{3}$ | D． | （$\sqrt{5}$）2=5 |
如图，在△ABC中，AB=AC，∠A=36°，BD为角平分线，且AE=DE．
4．已知四边形ABCD中，AC、BD相交于O，AB∥CD，则添加下列哪一个条件后，仍无法判定△AOB与△COD全等（ ）
| A． | AB=CD | B． | AD=BC | C． | AD∥BC | D． | OA=OC |
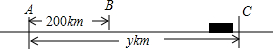用函数表达式表示下列变化过程中两个变量之间的关系，并指出其中的一次函数、正比例函数．