题目内容
8.已知:∠ACB=90°,AC=BC,AD⊥CM,BE⊥CM,垂足分别为D,E,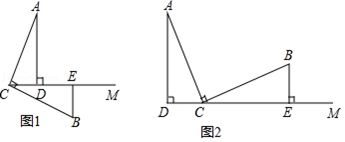
(1)如图1,把下面的解答过程补充完整,并在括号内注明理由.
①线段CD和BE的数量关系是:CD=BE;
②请写出线段AD,BE,DE之间的数量关系并证明.
解:①结论:CD=BE.
理由:∵AD⊥CM,BE⊥CM,
∴∠ACB=∠BEC=∠ADC=90°,
∴∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE
在△ACD和△CBE中,($\left\{\begin{array}{l}{∠ADC=∠BEC}\\{∠ACD=∠CBE}\\{AC=BC}\end{array}\right.$)
∴△ACD≌△CBE,(AAS)
∴CD=BE.
②结论:AD=BE+DE.
理由:∵△ACD≌△CBE,
∴AD=CE
∵CE=CD+DE=BE+DE,
∴AD=BE+DE.
(2)如图2,上述结论②还成立吗?如果不成立,请写出线段AD,BE,DE之间的数量关系.并说明理由.
分析 (1)根据同角的余角相等,全等三角形的判定和性质即可解决问题;
(2)结论:DE-BE=AD,只要证明△ACD≌△CBE即可解决问题;
解答 解:(1)∵AD⊥CM,BE⊥CM,
∴∠ACB=∠BEC=∠ADC=90°,
∴∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE
在△ACD和△CBE中,( $\left\{\begin{array}{l}{∠ADC=∠BEC}\\{∠ACD=∠CBE}\\{AC=BC}\end{array}\right.$)
∴△ACD≌△CBE,( AAS)
∴CD=BE.
②结论:AD=BE+DE.
理由:∵△ACD≌△CBE,
∴AD=CE
∵CE=CD+DE=BE+DE,
∴AD=BE+DE.
故答案为:∠CBE,$\left\{\begin{array}{l}{∠ADC=∠BEC}\\{∠ACD=∠CBE}\\{AC=BC}\end{array}\right.$,AAS,AD=CE.
(2)不成立,结论:DE-BE=AD.
理由:∵AD⊥CM,BE⊥CM,
∴∠ACB=∠BEC=∠ADC=90°,
∴∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE
在△ACD和△CBE中,
$\left\{\begin{array}{l}{∠ADC=∠BEC}\\{∠ACD=∠CBE}\\{AC=BC}\end{array}\right.$,
∴△ACD≌△CBE,( AAS)
∴AD=CE,CD=BE,
∴DE-BE=DE-DC=CE=AD.
点评 本题考查全等三角形的判定和性质,解题的关键是正确寻找全等三角形的全等条件,灵活运用知识解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.已知实数a,b满足|a-4|+$\sqrt{b-8}$=0,以a,b为边的等腰三角形的周长为( )
| A. | 12 | B. | 16 | C. | 20 | D. | 16或20 |
3. 周末小明从家出发沿金牛山公园散步,经过篮球场地看了一会篮球赛,然后继续散步了一段时间,最后回到家中,如图描述了小明散步过程中离家的距离s(米)与散步时间t(分)间的关系,下列说法错误的是( )
周末小明从家出发沿金牛山公园散步,经过篮球场地看了一会篮球赛,然后继续散步了一段时间,最后回到家中,如图描述了小明散步过程中离家的距离s(米)与散步时间t(分)间的关系,下列说法错误的是( )
 周末小明从家出发沿金牛山公园散步,经过篮球场地看了一会篮球赛,然后继续散步了一段时间,最后回到家中,如图描述了小明散步过程中离家的距离s(米)与散步时间t(分)间的关系,下列说法错误的是( )
周末小明从家出发沿金牛山公园散步,经过篮球场地看了一会篮球赛,然后继续散步了一段时间,最后回到家中,如图描述了小明散步过程中离家的距离s(米)与散步时间t(分)间的关系,下列说法错误的是( )| A. | 小明看篮球赛用时16分钟 | B. | 篮球场地距小明家600米 | ||
| C. | 小明离家最远距离为1200米 | D. | 小明从家出发到回家共用时32分钟 |
20.要使二次根式$\sqrt{x-3}$有意义,则x的值可以为( )
| A. | -2 | B. | 4 | C. | 2 | D. | 0 |
17.为了了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:
(1)根据上表的数据,写出用t表示Q的关系式;
(2)汽车行驶5h后,油箱中的剩余油量是多少?
(3)若汽车油箱中剩余油量为55L,则汽车行驶了多少小时?
(4)若该种汽车油箱只装了46L汽油,汽车以100km/h的速度在一条全长700公里的高速公路上匀速行驶,请问它在中途不加油的情况下能从高速公路起点开到高速公路终点吗,为什么?
| 汽车行驶时间t(h) | 0 | 1 | 2 | 3 | … |
| 油箱剩余油量Q(L) | 100 | 94 | 88 | 82 | … |
(2)汽车行驶5h后,油箱中的剩余油量是多少?
(3)若汽车油箱中剩余油量为55L,则汽车行驶了多少小时?
(4)若该种汽车油箱只装了46L汽油,汽车以100km/h的速度在一条全长700公里的高速公路上匀速行驶,请问它在中途不加油的情况下能从高速公路起点开到高速公路终点吗,为什么?
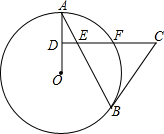 如图,CB是⊙O的切线,切点为B,CD⊥半径OA于D,交弦AB于点E,交⊙O于点F.
如图,CB是⊙O的切线,切点为B,CD⊥半径OA于D,交弦AB于点E,交⊙O于点F.