题目内容
5.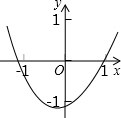 已知函数y=(x-a)(x-b)(其中a>b)的图象如图所示,则函数y=ax+b的图象可能正确的是( )
已知函数y=(x-a)(x-b)(其中a>b)的图象如图所示,则函数y=ax+b的图象可能正确的是( )| A. | 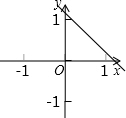 | B. | 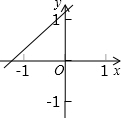 | C. | 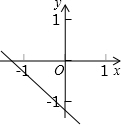 | D. | 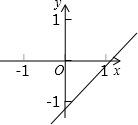 |
分析 由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线中自变量x=1及x=-1的情况进行推理,进而对所得结论进行判断.
解答 解:∵y=(x-a)(x-b)=x2-(a+b)x+ab,
∵抛物线的开口向上知a>0,与y轴的交点为在y轴负半轴上,∴ab<0,
∵对称轴在y轴的左侧,二次项系数>0,∴-(a+b)>0.
∴a+b<0,
∵a>b,
∴a>0,b<0,
∴y=ax+b的图象是D选项,
故选D.
点评 本题考查的是二次函数图象与系数的关系,掌握二次函数的性质、灵活运用数形结合思想是解题的关键,解答时,要熟练运用抛物线上的点的坐标满足抛物线的解析式.

练习册系列答案
相关题目
15.已知二元一次方程3x-y=1,当x=2时,y-8等于( )
| A. | 5 | B. | -3 | C. | -7 | D. | 7 |
13.某公司需招聘一名公关人员.对甲、乙两位应试者进行了面试和笔试,他们的成绩(百分制)如表所示.公司规定,面试成绩与笔试成绩的权重分别为6和4,请计算甲、乙两人各自的平均成绩,谁将被录取?
| 应试者 | 面试 | 笔试 |
| 甲 | 80 | 90 |
| 乙 | 90 | 80 |
20.线段EF是由线段PQ平移得到的,点P(-1,3)的对应点为E(4,7),则点Q(-3,1)的对应点F的坐标是( )
| A. | (-8,-3) | B. | (-2,-2) | C. | (2,5) | D. | (-6,-1) |
15.用一段长为30m的篱笆围成一个一边靠墙(长度不限)的菜园ABCD,并在垂直于墙的一边留一个1m宽的门,则平行于墙的篱笆长为( )时,菜园面积最大.
| A. | 15m | B. | 16m | C. | 15.5m | D. | 14m |
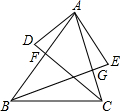 已知,△ABC中,BE⊥AC于G,CD⊥AB于F,BA=BE,CA=CD,以下结论:①∠D=∠E;②DF=GE;③$\frac{AF}{AG}$=$\frac{AC}{AB}$;④$\frac{DF}{CF}$=$\frac{EG}{BG}$,其中正确的有①③④(填上你认为所有正确结论的序号).
已知,△ABC中,BE⊥AC于G,CD⊥AB于F,BA=BE,CA=CD,以下结论:①∠D=∠E;②DF=GE;③$\frac{AF}{AG}$=$\frac{AC}{AB}$;④$\frac{DF}{CF}$=$\frac{EG}{BG}$,其中正确的有①③④(填上你认为所有正确结论的序号).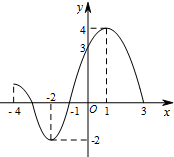 已知某函数图象如图所示,请回答下列问题:
已知某函数图象如图所示,请回答下列问题: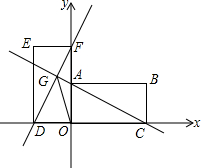 如图,直线y=-$\frac{1}{2}$x+1交y轴于A点,交x轴于C点,以A,O,C为顶点作矩形AOCB,将矩形AOCB绕O点逆时针旋转90°,得到矩形DOFE,直线AC交直线DF于G点.
如图,直线y=-$\frac{1}{2}$x+1交y轴于A点,交x轴于C点,以A,O,C为顶点作矩形AOCB,将矩形AOCB绕O点逆时针旋转90°,得到矩形DOFE,直线AC交直线DF于G点.