题目内容
12.仔细解答下列不等式组:(1)$\left\{\begin{array}{l}{2x>10-3x}\\{5+x≥3}\end{array}\right.$
(2)$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1}\\{1-3(x-1)<8-x}\end{array}\right.$.
分析 (1)先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可;
(2)先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:(1)$\left\{\begin{array}{l}{2x>10-3x①}\\{5+x≥3②}\end{array}\right.$
∵解不等式①得:x>2,
解不等式②得:x≥-2,
∴不等式组的解集为x>2;
(2)$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1①}\\{1-3(x-1)<8-x②}\end{array}\right.$
∵解不等式①得:x≤1,
解不等式②得:x>-2,
∴不等式组的解集为-2<x≤1.
点评 本题考查了解一元一次不等式组的应用,能根据不等式的解集找出不等式组的解集是解此题的关键,难度适中.

练习册系列答案
相关题目
7.下列式子中,是不等式的有( )
①2x=7;②3x+4y;③-3<2;④2a-3≥0;⑤x>1;⑥a-b>1.
①2x=7;②3x+4y;③-3<2;④2a-3≥0;⑤x>1;⑥a-b>1.
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 1个 |
17.下列说法正确的是( )
| A. | 若原命题为真,则其逆命题也为真 | |
| B. | 若原命题为假,则其逆命题也为假 | |
| C. | 若原命题为真,则其逆命题不一定为真 | |
| D. | 以上都不对 |
4.下列调查方式,合适的是( )
| A. | 要了解一批灯泡的使用寿命,选择全面调查 | |
| B. | 要了解某市初中生的“体重指数”,选择全面调查 | |
| C. | 要了解湖南卫视“我是歌手”的收视率,选择抽样调查 | |
| D. | 要了解某班20名学生的视力状况,选择抽样调查 |
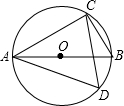 如图,已知AB为⊙O的直径,∠CAB=30°,则∠ADC=60度.
如图,已知AB为⊙O的直径,∠CAB=30°,则∠ADC=60度.