题目内容
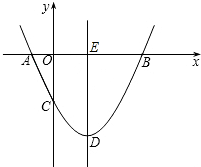 如图,抛物线y=
如图,抛物线y=| 1 |
| 2 |
考点:轴对称-最短路线问题,二次函数的性质,相似三角形的判定与性质
专题:
分析:首先可求得二次函数的顶点坐标,再求得C关于x轴的对称点C′,求得直线C′D的解析式,与x轴的交点的横坐标即是m的值,再利用相似三角形的判定和性质求解即可.
解答: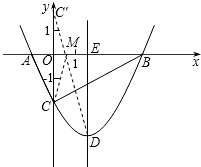 解:∵点A(-1,0)在抛物线y=
解:∵点A(-1,0)在抛物线y=
x2+bx-2上,
∴
×(-1)2+b×(-1)-2=0,
∴b=-
,
∴抛物线的解析式为y=
x2-
x-2,
∴顶点D的坐标为(
,-
),
作出点C关于x轴的对称点C′,则C′(0,2),OC′=2
连接C′D交x轴于点M,
根据轴对称性及两点之间线段最短可知,MC+MD的值最小.
设抛物线的对称轴交x轴于点E.
∵ED∥y轴,
∴∠OC′M=∠EDM,∠C′OM=∠DEM
∴△C′OM∽△DEM.
∴
=
,
即
=
,
∴m=
.
故答案为:
.
 解:∵点A(-1,0)在抛物线y=
解:∵点A(-1,0)在抛物线y=| 1 |
| 2 |
∴
| 1 |
| 2 |
∴b=-
| 3 |
| 2 |
∴抛物线的解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
∴顶点D的坐标为(
| 3 |
| 2 |
| 25 |
| 8 |
作出点C关于x轴的对称点C′,则C′(0,2),OC′=2
连接C′D交x轴于点M,
根据轴对称性及两点之间线段最短可知,MC+MD的值最小.
设抛物线的对称轴交x轴于点E.
∵ED∥y轴,
∴∠OC′M=∠EDM,∠C′OM=∠DEM
∴△C′OM∽△DEM.
∴
| OM |
| EM |
| OC′ |
| ED |
即
| m | ||
|
| 2 | ||
|
∴m=
| 24 |
| 41 |
故答案为:
| 24 |
| 41 |
点评:本题着重考查了待定系数法求二次函数解析式,轴对称性质以及相似三角形的性质,关键在于求出函数表达式,作出辅助线,找对相似三角形.

练习册系列答案
相关题目
 如图,下列说法中正确的是( )
如图,下列说法中正确的是( )| A、OA的方向是西偏北26°48' |
| B、OA的方向是北偏西63°12' |
| C、OA的方向是北偏西26°48' |
| D、OA的方向是北偏西26°88' |
 如图所示,△ABC中,∠C=90°,AM平分∠CAB,BC=16cm,CM:MB=3:5,求点M到AB的距离.
如图所示,△ABC中,∠C=90°,AM平分∠CAB,BC=16cm,CM:MB=3:5,求点M到AB的距离.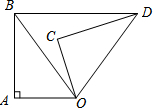 如图,在△OAB中,∠A=90°,△OCD是把△OAB以O为旋转中心,顺时针旋转而得到的(其中C与A对应),记旋转角为α,∠OBA为β.
如图,在△OAB中,∠A=90°,△OCD是把△OAB以O为旋转中心,顺时针旋转而得到的(其中C与A对应),记旋转角为α,∠OBA为β.