题目内容
15.现定义运算“△”,对于任意有理数a、b,都有a△b=a2-ab+b,例如:3△5=32-3×5+5=11,请根据上述知识解决问题:(1)(x-1)△(2+x);
(2)若(1)的代数式值大于6而小于9,求x的取值范围.
分析 (1)根据题意得出原式=(x-1)2-(x-1)(2+x)+(2+x),化简即可;
(2)根据题意得出不等式组,求出不等式组的解集即可.
解答 解:(1)(x-1)△(2+x)
=(x-1)2-(x-1)(2+x)+(2+x)
=x2-2x+1-2x-x2+2+x+2+x
=-2x+5;
(2)由题意得不等式组$\left\{\begin{array}{l}{-2x+5>6①}\\{-2x+5<9②}\end{array}\right.$
解不等式①得,x<-$\frac{1}{2}$,
解不等式②得,x>-2,
所以x的取值范围是-2<x<-$\frac{1}{2}$.
点评 本题考查了整式的混合运算,解一元一次不等式组的应用,能得出不等式组是解此题的关键,难度适中.

练习册系列答案
相关题目
6.若实数$\sqrt{7}$,$\frac{2}{3}$,0,$\frac{22}{33}$,-0.628,$\sqrt{36}$,3.020 020 002…(每相邻两个2之间0的个数逐渐多1)中,属于正无理数的共有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
3.下列说法正确的是( )
| A. | 平面内,过一点能作已知直线的一条平行线 | |
| B. | 平面内,过一点能作已知直线的一条垂线 | |
| C. | 射线AB的端点是A和B | |
| D. | 边长相等的多边形是正多边形 |
20.不等式2x-4<0的解集是( )
| A. | x<2 | B. | x>2 | C. | x≤2 | D. | x≥2 |
4.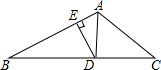 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=28,DE=4,AC=6,则AB的长是( )
如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=28,DE=4,AC=6,则AB的长是( )
 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=28,DE=4,AC=6,则AB的长是( )
如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=28,DE=4,AC=6,则AB的长是( )| A. | 8 | B. | 10 | C. | 12 | D. | 不能确定 |
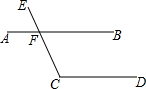 如图,AB∥CD,CE交AB于点F.若∠AFE=48°,则∠ECD=132°.
如图,AB∥CD,CE交AB于点F.若∠AFE=48°,则∠ECD=132°.