题目内容
20. 如图所示,已知在三角形纸片ABC中,BC=3,AC=4,∠BCA=90°,在AC上取一点E,BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则CD的长度为( )
如图所示,已知在三角形纸片ABC中,BC=3,AC=4,∠BCA=90°,在AC上取一点E,BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则CD的长度为( )| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
分析 先在Rt△ABC中根据勾股定理求得AB=5,然后由翻折的性质可知BD=AB=5,最后根据CD=BD-BC求解即可.
解答 解:∵BC=3,AC=4,∠BCA=90°,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=5.
由翻折的性质可知:BD=AB=5.
∴CD=BD-BC=5-3=2.
故选:B.
点评 本题主要考查的是翻折变换、勾股定理的应用,由翻折的性质求得BD=AB=5是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
15.下列计算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | $\sqrt{(-2)^{2}}$=-2 | C. | $\root{3}{27}$=9 | D. | $\root{3}{1{0}^{-3}}$=0.1 |
12.下列各数中的无理数是( )
| A. | $\frac{1}{9}$ | B. | 0.9 | C. | $\sqrt{9}$ | D. | $\root{3}{9}$ |
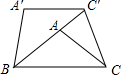 如图,将△ABC绕点B逆时针旋转40°,得到△A′B′C′,若点C′恰好落在边BA的延长线上,且A′C′∥BC,连接CC′,则∠ACC′=30度.
如图,将△ABC绕点B逆时针旋转40°,得到△A′B′C′,若点C′恰好落在边BA的延长线上,且A′C′∥BC,连接CC′,则∠ACC′=30度.
 (1)如图,点D在△ABC中,写出图中所有三角形:△ABD,△ADC,△BDC,△ABC
(1)如图,点D在△ABC中,写出图中所有三角形:△ABD,△ADC,△BDC,△ABC