题目内容
如图,在△ABC中,AB=AC,∠B=60°,∠FAC、∠ECA是△ABC的两个外角,AD平分∠FAC,CD平分∠ECA.求证:四边形ABCD是菱形.
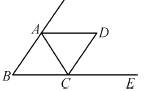
证明:∵∠B=60°,AB=AC,
∴△ABC为等边三角形,
∴AB=BC,∠BAC=∠ACB=60°,
∠FAC=∠ACE=120°.
又∵AD平分∠FAC,CD平分∠ECA,
∴∠FAD=∠ECD=60°,
∴AD∥BC,CD∥AB,
∴四边形ABCD是平行四边形.
∵AB=BC,∴四边形ABCD是菱形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
圆的有关概念
| 圆的定义 | 定义1:在一个平面内,一条线段绕着它固定的一个端点旋转一周,另一个端点所形成的图形叫做圆. |
| 定义2:圆是到定点的距离① 定长的所有点组成的图形. | |
| 弦 | 连接圆上任意两点的② 叫做弦. |
| 直径 | 直径是经过圆心的③ ,是圆内最④ 的弦. |
| 弧 | 圆上任意两点间的部分叫做弧,弧有⑤ 之分,能够完全重合的弧叫做⑥ . |
| 等圆 | 能够重合的两个圆叫做等圆. |
| 同心圆 | 圆心相同的圆叫做同心圆. |
 ,
, ,-
,- ,0中,无理数的个数是( )
,0中,无理数的个数是( ) ABC绕AC边的中点O旋转180°后与原三角形拼成的四边形一定是 .
ABC绕AC边的中点O旋转180°后与原三角形拼成的四边形一定是 .
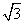 MN.
MN.

