Question

如图，在平行四边形ABCD中，∠C=60°，M、N分别是AD、BC的中点，BC=2CD.

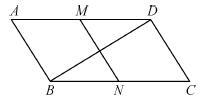
(1)求证：四边形MNCD是平行四边形；

(2)求证：BD=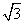MN.

Answer 1

证明：(1)∵四边形ABCD是平行四边形，

∴AD∥BC，AD＝BC.

∵M、N分别是AD、BC的中点，

∴MD＝NC，MD∥NC，

∴四边形MNCD是平行四边形.

(2)连接ND，

∵N是BC的中点，∴BN=CN.

∵BC=2CD，∠C=60°，∴△NCD是等边三角形.

∴ND＝NC,∠DNC＝∠NDC＝60°，

∴ND＝NB＝CN，

∴∠DBC＝∠BDN＝30°，

∴∠BDC＝∠BDN+∠NDC＝90°，

∴BD＝==CD.

∵四边形MNCD是平行四边形，∴MN＝CD,

∴BD＝MN.