题目内容
已知⊙O的直径AB与弦CD相交于点E,AE=6cm,BE=4cm,∠CEA=30°,求CD的长.
考点:垂径定理,含30度角的直角三角形,勾股定理
专题:
分析:如图,作辅助线;首先求出OC、OF;借助勾股定理求出CF的长度,即可解决问题.
解答: 解:如图,连接OC,过点O作OF⊥CD;
解:如图,连接OC,过点O作OF⊥CD;
则CF=DF;
∵AE=6,BE=4,
∴OB=
AB=5,OC=OB=5,
∴OE=5-4=1;
∵∠CEA=30°,
∴OF=
,由勾股定理得:
CF2=CO2-OF2
=25-
=
,
∴CF=
,
∴DC=2CF=3
.
 解:如图,连接OC,过点O作OF⊥CD;
解:如图,连接OC,过点O作OF⊥CD;则CF=DF;
∵AE=6,BE=4,
∴OB=
| 1 |
| 2 |
∴OE=5-4=1;
∵∠CEA=30°,
∴OF=
| 1 |
| 2 |
CF2=CO2-OF2
=25-
| 1 |
| 4 |
| 99 |
| 4 |
∴CF=
3
| ||
| 2 |
∴DC=2CF=3
| 11 |
点评:该题主要考查了垂径定理、勾股定理、含30°角的直角三角形的边角关系及其应用问题;解题的关键是作辅助线,灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
在比例尺为1:40000的莱州市地图上,文化东街的长度约为10cm,它的实际长度约为( )
| A、40m | B、400m |
| C、4000m | D、40000m |
下列语句正确的是( )
| A、延长线段AB到C,使BC=AC |
| B、反向延长线段AB,得到射线BA |
| C、取直线AB的中点 |
| D、连接A、B两点,并使直线AB经过C点 |
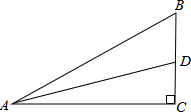 如图,在Rt△ABC中,BC=1,∠BAC=30°,AD是∠BAC的平分线交BC于D,∠C=90°.
如图,在Rt△ABC中,BC=1,∠BAC=30°,AD是∠BAC的平分线交BC于D,∠C=90°. 如图,在菱形ABCD中,∠A=135°,AB=
如图,在菱形ABCD中,∠A=135°,AB=
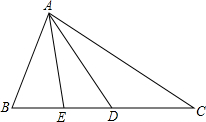 如图:在△ABC中,D是BC上一点,E是BD的中点,并且AB=DC,AE=
如图:在△ABC中,D是BC上一点,E是BD的中点,并且AB=DC,AE= 已知点C为∠AOB内一点,OM,ON分别平分∠AOC和∠BOC,则∠MON=
已知点C为∠AOB内一点,OM,ON分别平分∠AOC和∠BOC,则∠MON=