题目内容
 将半径为4cm的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为
将半径为4cm的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为考点:圆锥的计算,翻折变换(折叠问题)
专题:计算题
分析:作OC⊥AB于C,如图,根据折叠的性质得OC等于半径的一半,即OA=2OC,再根据含30度的直角三角形三边的关系得∠OAC=30°,则∠AOC=60°,所以∠AOB=120°,则利用弧长公式可计算出弧AB的长=
π,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长得到圆锥的底面圆的半径为
,然后根据勾股定理计算这个圆锥的高.
| 8 |
| 3 |
| 4 |
| 3 |
解答: 解:作OC⊥AB于C,如图,
解:作OC⊥AB于C,如图,
∵将半径为4cm的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,
∴OC等于半径的一半,即OA=2OC,
∴∠OAC=30°,
∴∠AOC=60°,
∴∠AOB=120°,
弧AB的长=
=
π,
设圆锥的底面圆的半径为r,
∴2πr=
π,解得r=
,
∴这个圆锥的高=
=
(cm).
故答案为
.
 解:作OC⊥AB于C,如图,
解:作OC⊥AB于C,如图,∵将半径为4cm的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,
∴OC等于半径的一半,即OA=2OC,
∴∠OAC=30°,
∴∠AOC=60°,
∴∠AOB=120°,
弧AB的长=
| 120π•4 |
| 180 |
| 8 |
| 3 |
设圆锥的底面圆的半径为r,
∴2πr=
| 8 |
| 3 |
| 4 |
| 3 |
∴这个圆锥的高=
42-(
|
8
| ||
| 3 |
故答案为
8
| ||
| 3 |
点评:本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若二次根式
有意义,则x的取值范围是( )
| 2-x |
| A、x≥2 | B、x>2 |
| C、x≤2 | D、x<2 |
 2014年1月10日,绿色和平发布了全国74个城市PM2.5浓度年均值排名和相应的最大日均值,其中浙江省六个地区的浓度如图(舟山的最大日均值条形图缺损)以下说法中错误的是( )
2014年1月10日,绿色和平发布了全国74个城市PM2.5浓度年均值排名和相应的最大日均值,其中浙江省六个地区的浓度如图(舟山的最大日均值条形图缺损)以下说法中错误的是( )| A、这6个地区中,最大日均值最高的是绍兴 |
| B、杭州的年均值约是舟山的2倍 |
| C、舟山的最大日均值不一定低于丽水的最大日均值 |
| D、这6个地区中,低于国家环境空气质量标准规定的年均值35微克每立方米的地区只有舟山 |
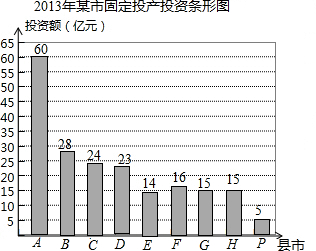 某地统计局对2013年各县市的固定资产投资情况进行了统计,并绘成了如图,请根据相关信息解答下列问题:下列结论不正确的是( )
某地统计局对2013年各县市的固定资产投资情况进行了统计,并绘成了如图,请根据相关信息解答下列问题:下列结论不正确的是( )| A、2013年某市固定资产投资总额为200亿元 |
| B、2013年某市各单位固定资产投资额的中位数是16亿元 |
| C、2013年A县固定资产投资额为占总额的30% |
| D、2013年固定资产投资扇形统计图中表示A地的扇形的圆心角为110° |
 二次函数y=
二次函数y=