Question

已知：如图，AD平分∠BAC，M是BC的中点，MF∥AD交CA的延长线于F，求证：BE=CF．

Answer 1

分析：延长EM到G，使MG=EM，连接GC，推出∠1=∠F，证△BEM≌△CGM，推出BE=CG，∠1=∠G=∠F，推出CF=CG，即可得出答案．

解答：证明：延长EM到G，使MG=EM，连接GC，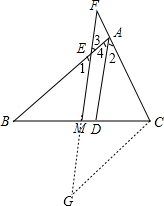
∵MF∥AD，
∴∠2=∠F，∠4=∠3，
∵AD平分∠BAC，
∴∠2=∠4，
∵∠1=∠3，
∴∠1=∠F，
∵M是BC的中点，
∴BM=CM，
∵在△BEM和△CGM中，

EM=MG ∠BME=∠GMC BM=MC

，
∴△BEM≌△CGM（SAS），
∴BE=CG，∠1=∠G，
∵∠1=∠F，
∴∠F=∠G，
∴CG=CF，
∴BE=CF．

点评：本题考查了平行线的性质，角平分线定义，全等三角形的性质和判定，等腰三角形的判定，对顶角相等等知识点的综合运用．