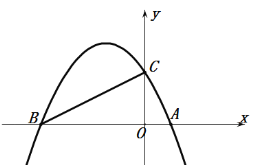题目内容
【题目】如图，利用一面院墙，用篱笆围成一个外形为矩形的花圃，花圃的面积为S平方米，平行于院墙的一边长为x米.
（1）若院墙可利用最大长度为10米，篱笆长为24米，花圃中间用一道篱笆间隔成两个小矩形，求S与x之间的函数关系；
（2）在（1）的条件下，若围成的花圃面积为45平方米，求AB的长；
（3）在（1）的条件下，能否围成面积比45平方米更大的花圃？请说明理由.
【答案】（1）
；（2）AB=5米；（3）故能围成面积比45平方米更大的花圃.
【解析】
（1）根据矩形的面积=长×宽，得出S与x的函数关系式；
（2）根据（1）的函数关系式，将S=45代入其中，求出x的值即可；
（3）根据二次函数的性质求出自变量取值范围内的最值，大于45平方米则能，否则不能．
解：(1)
(
)
(2)当S=45时, 
解之得, 
∵
不合题意，舍去.∴AB=5米
（3）由于
，当
时，
随
的增大而增大.
∴当x=10时，
>45.
故能围成面积比45平方米更大的花圃.
练习册系列答案
相关题目
【题目】在平面直角坐标系xOy中，抛物线C1：y＝﹣x2+2x．
（1）补全表格：
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
y＝﹣x2+2x | （1，1） |
|
| （0，0） |
（2）将抛物线C1向上平移3个单位得到抛物线C2，请画出抛物线C1，C2，并直接回答：抛物线C2与x轴的两交点之间的距离是抛物线C1与x轴的两交点之间距离的多少倍．
