题目内容
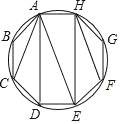
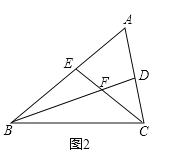
【题目】如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F连接AE、DE、DF.
(1)证明:∠E=∠C;
(2)若∠E=58°,求∠BDF的度数.

【答案】(1)证明见解析;(2)∠BDF=116°.
【解析】
(1)连接AD,已知AB是⊙O的直径,根据直径所对的圆周角是直角即可得∠ADB=90°,即AD⊥BC;由CD=BD可得AD垂直平分BC,根据线段垂直平分线的性质可得AB=AC,所以∠B=∠C;根据同弧所对的圆周角相等可得∠B=∠E,由此即可证得∠E=∠C;(2)已知四边形AEDF是⊙O的内接四边形,根据圆内接四边形对角互补可得∠AFD=180°﹣∠E,由邻补角的定义可得∠CFD=180°﹣∠AFD,从而求得∠CFD=∠E=58°,再由∠BDF=∠C+∠CFD即可求得∠BDF的度数.
(1)连接AD,

∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵CD=BD,
∴AD垂直平分BC,
∴AB=AC,
∴∠B=∠C,
又∵∠B=∠E,
∴∠E=∠C;
(2)∵四边形AEDF是⊙O的内接四边形,
∴∠AFD=180°﹣∠E,
又∵∠CFD=180°﹣∠AFD,
∴∠CFD=∠E=58°,
又∵∠E=∠C=58°,
∴∠BDF=∠C+∠CFD=116°.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目