Question

【题目】已知：在平面直角坐标系中，△ABC的顶点A、C分别在y轴、x轴上，且∠ACB=90°，AC=BC．

（1）如图1，当，点B在第四象限时，则点B的坐标为 ；

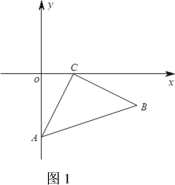
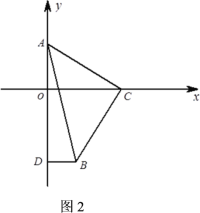
（2）如图2，当点C在x轴正半轴上运动，点A在y轴正半轴上运动，点B在第四象限时，作BD⊥y轴于点D，试判断与哪一个是定值，并说明定值是多少？请证明你的结论．（温馨提示：本题定值就是某一个固定的常数值）

Answer 1

【答案】（1）B点坐标为：(，)；（2）是定值，且为1，证明见解析

【解析】

（1）作BD⊥轴，交轴于D点，通过证明△OAC△DCB再利用全等三角形性质进一步求解即可；

（2）作BE⊥轴于E，则四边形ODBE为矩形，先证明出△CEB△AOC，然后利用全等三角形性质以及矩形性质进一步得出OC=AO+BD，据此进一步分析证明即可.

（1）如图所示，作BD⊥轴，交轴于D点，

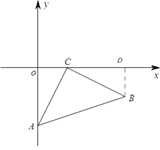
∵∠ACB=90°，

∴∠OCA+∠DCB=90°，

∵∠OCA+∠OAC=90°，

∴∠DCB=∠OAC，

在△OAC与△DCB中，

∵∠AOC=∠CDB，∠DCB=∠OAC，AC=BC，

∴△OAC△DCB，

∵A点坐标为(0，)，C点坐标为(1，0)，

∴CD=OA=2，BD=OC=1，

∴OD=3，

∴B点坐标为：(，)，

故答案为：(，)；

（2）是定值，且为1，证明如下：

作BE⊥轴于E，则四边形ODBE为矩形，

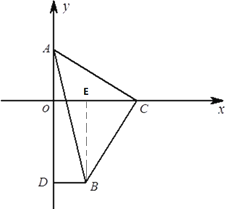
∵∠ACO+∠BCO=90°，∠ACO+∠OAC=90°，

∴∠BCO=∠CAO，

在△CEB和△AOC中，

∵，

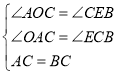∴△CEB△AOC，

∴EC=OA，

∵四边形ODBE为矩形，

∴OE=BD，

∵OC=OE+EC，

∴OC=AO+BD，

∴OC－BD =AO，

∴

∴存在定值，且为1.