题目内容
17.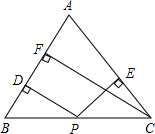 如图所示,在等腰三角形ABC中.底边BC上有任意一点P,则点P到两腰的距离之和等于定长(腰上的高),即PD+PE=CF,若点P在BC的延长线上,那么PD,PE和CF存在什么等式关系?写出你的猜想并加以证明.(提示:有三个角等于90°的四边形是长方形.)
如图所示,在等腰三角形ABC中.底边BC上有任意一点P,则点P到两腰的距离之和等于定长(腰上的高),即PD+PE=CF,若点P在BC的延长线上,那么PD,PE和CF存在什么等式关系?写出你的猜想并加以证明.(提示:有三个角等于90°的四边形是长方形.)
分析 先过点C作CG⊥PD于G,构造矩形CFDG,得出CF=DG,再判定△PCG≌△PCE(AAS),得出PG=PE,进而得到PD=DG+PG=CF+PE.
解答  解:PD=CF+PE.
解:PD=CF+PE.
证明:如图所示,过点C作CG⊥PD于G,则∠CGD=90°,
∵CF⊥AB,PD⊥AB,
∴∠CFD=∠GDF=90°,
∴四边形CFDG是长方形,
∴CF=DG,
∵AB=AC,
∴∠B=∠ACB,
又∵CG∥AB,
∴∠PCG=∠B,
又∵∠ACB=∠PCE,
∴∠PCG=∠PCE,
∵PE⊥AE,
∴∠PGC=∠E=90°,
在△PCG和△PCE中,
$\left\{\begin{array}{l}{∠PGC=∠E}\\{∠PCG=∠PCE}\\{CP=CP}\end{array}\right.$,
∴△PCG≌△PCE(AAS),
∴PG=PE,
∴PD=DG+PG=CF+PE.
点评 本题主要考查了矩形的判定与全等三角形的判定与性质的综合应用,解决问题的关键是作辅助线构造矩形和全等三角形,根据矩形对边相等以及全等三角形对应边相等计算推导.

练习册系列答案
相关题目
 如图,直线AB与直线CD相交于点O,∠AOC=25°,∠COE=90°,OF是∠COE内一条射线,OE平分∠FOB.
如图,直线AB与直线CD相交于点O,∠AOC=25°,∠COE=90°,OF是∠COE内一条射线,OE平分∠FOB.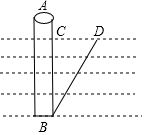 桥梁工程师想探知50m高的一根桥桩是否与地面垂直,他用铅锤系着一根与桥桩等长的绳子沉到桥桩底部,这时发现水面向上露出10m(AC),再斜拉绳子的端点A到水面的D处,测得CD=30m,根据这位工程师测得的数据,判断桥桩与地面是否垂直.
桥梁工程师想探知50m高的一根桥桩是否与地面垂直,他用铅锤系着一根与桥桩等长的绳子沉到桥桩底部,这时发现水面向上露出10m(AC),再斜拉绳子的端点A到水面的D处,测得CD=30m,根据这位工程师测得的数据,判断桥桩与地面是否垂直.
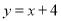 分别与x轴、y轴相交与点M、N,边长为2的正方形OABC一个顶点O在坐标系的原点,直线AN与MC相交与点P,若正方形绕着点O旋转一周,则点P到点(0,2)长度的最小值是( )
分别与x轴、y轴相交与点M、N,边长为2的正方形OABC一个顶点O在坐标系的原点,直线AN与MC相交与点P,若正方形绕着点O旋转一周,则点P到点(0,2)长度的最小值是( )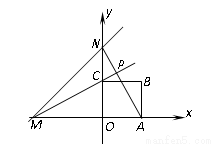
 B.
B. 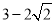 C.
C. 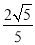 D. 1
D. 1