题目内容
如图，在三角形ABC中，∠C=90度，DE⊥AB，若DE=3，BC=5，AE=4，求AC的长．
解：∵DE⊥AB，
∴∠AED=90°，
∴∠C=∠AED，
∵∠A=∠A，
∴△AED∽△ACB，
∴
，
∴
，
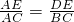∴AC=
．
分析：利用由两对角相等的两个三角形相似可证明△AED∽△ACB，由相似三角形的性质：对应边的比值相等即可求出AC的长．
点评：本题考查了相似三角形的判定和性质，是中考常见题型，比较简单．
∴∠AED=90°，
∴∠C=∠AED，
∵∠A=∠A，
∴△AED∽△ACB，
∴
，∴
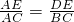，∴AC=
．分析：利用由两对角相等的两个三角形相似可证明△AED∽△ACB，由相似三角形的性质：对应边的比值相等即可求出AC的长．
点评：本题考查了相似三角形的判定和性质，是中考常见题型，比较简单．
练习册系列答案
相关题目
如图，在三角形ABC中，AD⊥BC，BE⊥AC，CF⊥AB，BC=16，AD=3，BE=4，CF=6，你能求出三角形ABC的周长吗？
43、如图，在三角形ABC中，AD是BC边上的中线，三角形ABD的周长比三角形ACD的周长小5，你能求出AC与AB的边长的差吗？
29、如图，在三角形ABC中∠1+∠2=180°，∠3=∠B以下是某同学说明∠ADE=∠ACB的推理过程或理由，请你在横线上补充完整其推理过程或理由．
如图，在三角形ABC中，AB=24，AC=18，D是AC上一点AD=12，在AB上取一点E，使A、D、E三点组成的三角形与ABC相似，则AE=
如图，在三角形ABC中，先按要求画图，再回答问题：