Question

已知点A、B分别是x轴、y轴上的动点，点C、D是某函数图象上的点，当四边形ABCD（A、B、C、D各点依次排列）为正方形时，称这个正方形为此函数图象的伴侣正方形．如图，正方形ABCD是反比例函数y=

2

x

图象上的其中一个伴侣正方形．则这个伴侣正方形的边长是

2

．

Answer 1

分析：过C作CF垂直于y轴，过D作DE垂直于x轴，利用垂直的定义得到三个角为直角，再由正方形的性质得到四条边相等，四个角为直角，利用同角的余角相等得到三个角相等，利用AAS得出△BFC≌△AOB≌△DAE，利用全等三角形的对应边相等得到FC=OB=AE，FB=OA=DE，再由C、D都在反比例函数y=

2

x

图象上，故设C（a，

2

a

），D（b，

2

b

），由OA=OE-AE列出关系式，再由OF=FB+OB列出另一个关系式，联立两关系式求出a与b的值，确定出CF与FB的长，在直角三角形FCB中，利用勾股定理求出BC的长，即为正方形ABCD的边长．

解答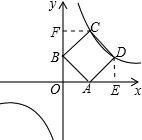：解：过C作CF⊥y轴，交y轴于点F，过D作DE⊥x轴，交x轴于点E，
∴∠CFB=∠DEA=∠AOB=90°，
∴∠FCB+∠FBC=90°，∠BAO+∠ABO=90°，
∵四边形ABCD为正方形，
∴CB=AB=AD，∠CBA=∠BAD=90°，
∴∠FBC+∠ABO=90°，∠BAO+∠DAE=90°，
∴∠FCB=∠ABO=∠DAE，
∴△BFC≌△AOB≌△DAE，
∴FC=OB=AE，FB=OA=DE，
由C、D都在反比例函数y=

2

x

图象上，故设C（a，

2

a

），D（b，

2

b

），
∴FC=OB=AE=a，FB=OA=DE=

2

b

，
又FB=DE=OA=OE-AE=b-a，
∴

2

b

=b-a，即b²-ab=2①，
又OF=FB+OB=

2

a

，
∴b-a+a=

2

a

，即ab=2②，
②代入①得：b²=4，
解得：b=2，
将b=2代入②得：a=1，
∴CF=1，FB=b-a=1，
在Rt△BCF中，根据勾股定理得：BC=

CF2+BF2

=

2

，
则这个伴侣正方形的边长为

2

．
故答案为：

2

点评：此题属于一次函数综合题，同时又属于新定义题，比较复杂，先要正确理解伴侣正方形的意义，特别要注意的是正方形的顶点所处的位置，因为涉及到相关点的坐标，所以过某一点作坐标轴的垂线是必不可少的，再利用正方形的性质和全等三角形的知识确定相关点的坐标即可求解．