Question

【题目】如图，在平面直角坐标系中，B点坐标为（﹣2，0），A点坐标为（a，b），且b≠0．

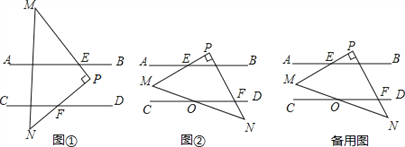
（1）若b＞0，且∠ABO：∠BAO：∠AOB＝10：5：21，在AB上取一点C，使得y轴平分∠COA．在x轴上取点D，使得CD平分∠BCO，过C作CD的垂线CE，交x轴于E．

①依题意补全图形；

②求∠CEO的度数；

（2）若b是定值，过O作直线AB的垂线OH，垂足为H，则OH的最大值是　 　．（直接写出答案）

Answer 1

【答案】（1）①见解析；②12.5°；（2）2

【解析】

（1）①根据要求画出图形即可．
②如图1中，延长DC交y轴于T．利用三角形的内角和定理求出∠A，再证明∠T＝∠A即可解决问题．
（2）利用垂线段最短即可解决问题．

解：（1）①图形如图1所示．

②如图1中，延长DC交Y轴于T．

∵∠ABO：∠BAO：∠AOB＝10：5：21，

∴∠A＝×180°＝25°，

∵CD平分∠BCO，OT平分∠AOC，

设∠BCD＝∠OCD＝x，∠AOT＝∠COT＝y，

则有2x＝∠A+2y，x＝y+∠OTC，

∴∠OTC＝∠A＝12.5°，

∵EC⊥CD，

∴∠ECT＝90°，

∴∠CEO＝∠OTC＝12.5°．

（2）如图2中，作OH⊥AB于H．

∵B（﹣2，0），

∴OB＝2，

∵OH≤OB，

∴OH≤2，

∴OH的最大值为2．

故答案为2．