题目内容
 如图所示:
如图所示:(1)若AB∥CD,猜测∠BED与∠B,∠D之间的关系是
(2)若AB∥CD,∠B=40°,∠BED=70°,你能求出∠D的度数吗?
考点:平行线的性质
专题:
分析:(1)首先过点E作EF∥AB,可得AB∥EF∥CD,然后根据两直线平行,内错角相等,求得∠1=∠B,∠2=∠D,继而证得∠BED=∠B+∠D;
(2)由∠BED=∠B+∠D,∠B=40°,∠BED=70°,即可求得∠D的度数.
(2)由∠BED=∠B+∠D,∠B=40°,∠BED=70°,即可求得∠D的度数.
解答: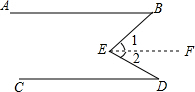 解:(1)∠BED=∠B+∠D.
解:(1)∠BED=∠B+∠D.
理由:过点E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠1=∠B,∠2=∠D,
∴∠BED=∠1+∠2=∠B+∠D;
故答案为:∠BED=∠B+∠D;
(2)∵∠BED=∠B+∠D,∠B=40°,∠BED=70°,
∴∠D=∠BED-∠B=30°.
 解:(1)∠BED=∠B+∠D.
解:(1)∠BED=∠B+∠D.理由:过点E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠1=∠B,∠2=∠D,
∴∠BED=∠1+∠2=∠B+∠D;
故答案为:∠BED=∠B+∠D;
(2)∵∠BED=∠B+∠D,∠B=40°,∠BED=70°,
∴∠D=∠BED-∠B=30°.
点评:此题考查了平行线的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
4a-a的计算结果是( )
| A、3 | B、3a | C、4 | D、4a |
-5的倒数是( )
| A、5 | ||
B、
| ||
C、-
| ||
| D、-5 |
 如图,如果AB∥CD,BC∥ED,那么∠B+∠D等于多少度?
如图,如果AB∥CD,BC∥ED,那么∠B+∠D等于多少度?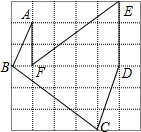 如图,这是由36个边长为1的小正方形拼成的方格图,依次连接小正方形的顶点A,B,C,D,E,F得线段AB,BC,CD,DE,EF,FA,请说出这些线段中的长度是有理数的有哪些,是无理数的有哪些,并在数轴上作出表示
如图,这是由36个边长为1的小正方形拼成的方格图,依次连接小正方形的顶点A,B,C,D,E,F得线段AB,BC,CD,DE,EF,FA,请说出这些线段中的长度是有理数的有哪些,是无理数的有哪些,并在数轴上作出表示 已知抛物线y=x2+bx+c的图象如图所示,则一元二次方程x2+bx+c=0的解是
已知抛物线y=x2+bx+c的图象如图所示,则一元二次方程x2+bx+c=0的解是