Question

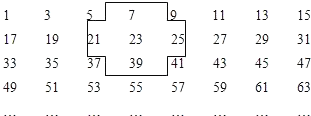
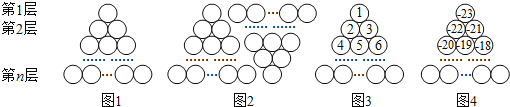
【题目】图1是由若干个小圆圈堆成的一个形如正三角形的图案，最上面一层有一个圆圈，以下各层均比上一层多一个圆圈，一共堆了n层．将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为，图3图4的中的圆圈共有14层.我们自上往下，在每个圆圈中都按图3的方式填上一串连续的正整数1，2，3，4，…，则最底层最左边这个圆圈中的数是__________；我们自上往下，在每个圆圈中都按图4的方式填上一串连续的整数﹣23，﹣22，﹣21，…，则图4中所有圆圈中各数的绝对值之和为__________.

Answer 1

【答案】92 3597

【解析】

（1）首先根据图3计算13层圆圈的个数，可得第14层第1个数；
（2）首先计算圆圈的个数，把所有数的绝对值相加即可．

解：（1）在14层中，我们自上往下，在每个圆圈中都按图3的方式填上一串连续的正整数1，2，3，4，…，根据题意，当有13层时，图中共有：

，

∴第14层最左边这个圆圈中的数是92；

（2））图4中共有14层，所有圆圈中共有个数，其中23个负数，1个0，81个正数，

∴图4中所有圆圈中各数的绝对值之和为：

．

故答案为92，3597.