Question

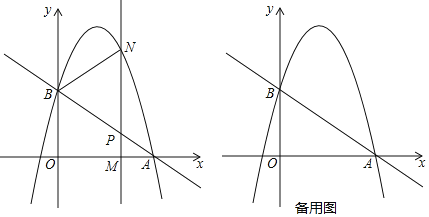
【题目】如图，抛物线过点， ． 为线段OA上一个动点（点M与点A不重合），过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N．

（1）求直线AB的解析式和抛物线的解析式；

（2）如果点P是MN的中点，那么求此时点N的坐标；

（3）如果以B，P，N为顶点的三角形与相似，求点M的坐标．

Answer 1

【答案】（1），；（2）N（，）；（3）M(，0)或M(，0) .

【解析】分析: （1）利用待定系数法求直线和抛物线解析式；

（2）先表示出N（m，- m2+m+2），P（m，-m+2），则计算出NP=-m2+4m，PM=-m+2，则利用NP=PM得到-m2+4m=-m+2，然后解方程求出m即可得到N点坐标；

（3）利用两点间的距离公式计算出AB=，BP=m，NP=-m2+4m，由于∠BPN=∠ABO，利用相似三角形的判定方法，当时，△BPN∽△OBA，则△BPN∽△MPA，即；当时，△BPN∽△ABO，则△BPN∽△APM，即，然后分别解关于m的方程即可得到对应的M点的坐标.

详解:

（1）解：设直线的解析式为（）

∵，

∴ 解得

∴直线的解析式为

∵抛物线经过点，

∴ 解得

∴

（2）∵轴， 设，

∴，

∵点是的中点

∴

∴

解得， （不合题意，舍去）

∴

（3）∵， ，

∴，

∴

∵

∴当与相似时，存在以下两种情况：

∴ 解得

∴

∴ ,解得

∴

点睛: 本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征、二次函数的性质和相似三角形的判定与性质；会利用待定系数法求函数解析式；灵活应用相似比表示线段之间的关系；理解坐标与图形的性质；会利用分类讨论的思想解决数学问题.