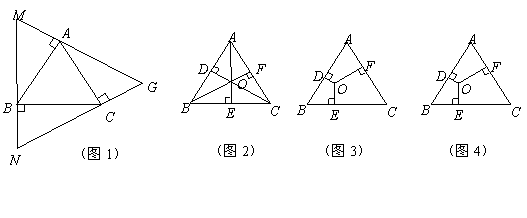
题目内容
已知:等边![]() 的边长为
的边长为![]() .
.
探究(1):如图1,过等边![]() 的顶点
的顶点![]() 依次作
依次作![]() 的垂线围成
的垂线围成![]() 求证:
求证:![]() 是等边三角形且
是等边三角形且![]() ;
;
探究(2):在等边![]() 内取一点
内取一点![]() ,过点
,过点![]() 分别作
分别作![]() 垂足分别为点
垂足分别为点![]()
①如图2,若点![]() 是
是![]() 的重心,我们可利用三角形面积公式及等边三角形性质得到两个正确结论(不必证明):结论1.
的重心,我们可利用三角形面积公式及等边三角形性质得到两个正确结论(不必证明):结论1.![]() ;结论2.
;结论2.![]() ;
;
②如图3,若点![]() 是等边
是等边![]() 内任意一点,则上述结论
内任意一点,则上述结论![]() 是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
 |
证明:如图1,![]() 为等边三角形
为等边三角形
![]()

![]()
∴![]()
![]()
![]()
同理:![]()
![]() 为等边三角形.
为等边三角形.
在![]() 中,
中,![]()
在![]() 中,
中,![]()
![]()
(2)![]() :结论1成立.
:结论1成立.
证明;方法一:如图2,连接![]()
由![]() =
=![]()
作![]() 垂足为
垂足为![]() ,
,
 则
则![]()
![]()
![]()
![]()
方法二:如图3,过点![]() 作
作![]() 分别交
分别交![]() 于点
于点![]() ,过点
,过点
![]() 作
作![]() 于点
于点![]() ,
,
![]()
![]() 是等边三角形
是等边三角形
![]()
![]()
![]()
![]() 四边形
四边形![]() 是矩形
是矩形
![]()
在![]() 中,
中,![]()
 在
在![]() 中,
中,![]()
在![]() 中,
中,![]()
![]()
![]()
(2)![]() 结论2成立.
结论2成立.
证明:方法一:如图4,过顶点![]() 依次作边
依次作边![]() 的垂线围成
的垂线围成![]() 由(1)得
由(1)得![]() 为等边三角形且
为等边三角形且![]() 分
分
过点![]() 分别作
分别作![]() 于
于![]() ,
,![]() 于
于![]() 于点
于点![]() 于点
于点![]()
由结论1得:
![]()
 又
又![]()
![]()
![]() 四边形
四边形![]() 为矩形
为矩形
![]()
![]()
同理:![]() ,
,![]()
![]()
方法二:(同结论1方法二的辅助线)
在![]() 中,
中,![]()
在![]() 中,
中,![]()
![]()
同理:![]()
![]()
=![]()
=![]()
由结论1得:![]()
![]()
方法三:如图5,连接![]() ,根据勾股定理得:
,根据勾股定理得:
![]()

![]()
![]()
![]() :
:
![]()
![]()
![]()
整理得:![]()
![]()

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
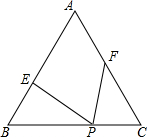 (2013•海门市一模)已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y.
(2013•海门市一模)已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y. ,点
,点 在
在 正半轴上,且
正半轴上,且 .动点
.动点 在线段
在线段 上从点
上从点 向点
向点 个单位的速度运动,设运动时间为秒.点M、N在
个单位的速度运动,设运动时间为秒.点M、N在 是等边三角形.
是等边三角形. 运动到与原点
运动到与原点 重合时的值;
重合时的值; 的中点
的中点 ,以
,以 为边在
为边在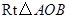 内部作如图2所示的矩形
内部作如图2所示的矩形 ,点
,点 在线段
在线段 ,请求出当
,请求出当 秒时,
秒时,