Question

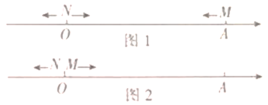
【题目】如图,数轴上A、B两点对应的有理数分别为8和12,点从点出发,以每秒1个单位长度的速度沿数轴正方向运动,点同时从原点出发,以每秒2个单位长度的速度沿数轴正方向运动.设运动时间为秒

(1)当时,用含的式子表示和;

(2)当时,求的值;

(3)当时,求的值.

Answer 1

【答案】（1）BP=12-（8+t）=4-t，AQ=8-2t．
（2）PQ=10-4=6；
（3）t的值是10或6．

【解析】

（1）先求出当0＜t＜4时，P点对应的有理数为8+t＜12，Q点对应的有理数为2t＜8，再根据两点间的距离公式即可求出BP，AQ的长；
（2）先求出当t=2时，P点对应的有理数为8+2=10，Q点对应的有理数为2×2=4，再根据两点间的距离公式即可求出PQ的长；
（3）由于t秒时，P点对应的有理数为8+t，Q点对应的有理数为2t，根据两点间的距离公式得出PQ=|2t-（8+t）|=|t-8|，根据PQ=AB列出方程，解方程即可．