题目内容
菱形ABCD的边长为2cm，∠A为45°，那么这个菱形的面积为________cm2．
2
分析：过D点作DE⊥AB，垂足为E，根据已知可求得DE的长，再根据面积公式求得菱形的面积．
解答：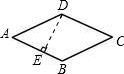
解：过D点作DE⊥AB，垂足为E，
∵AD=2cm，sinA=
=
，
∴DE=×2=cm．
∴菱形的面积=DE•AB=×2=2cm2．
故答案为2．
点评：本题考查了菱形的四条边相等的性质，以及对角线互相垂直平分的性质，还考查了菱形面积的计算，解答本题的关键是求出DE的长．
分析：过D点作DE⊥AB，垂足为E，根据已知可求得DE的长，再根据面积公式求得菱形的面积．
解答：
解：过D点作DE⊥AB，垂足为E，∵AD=2cm，sinA=
=，∴DE=
×2=cm．∴菱形的面积=DE•AB=
×2=2cm2．故答案为2
．点评：本题考查了菱形的四条边相等的性质，以及对角线互相垂直平分的性质，还考查了菱形面积的计算，解答本题的关键是求出DE的长．
练习册系列答案
相关题目
已知：如图，菱形ABCD的边长为4，∠A=60°，以点A为圆心，AD长为半径画弧，以点B为圆心，BC长为半径画弧，则图中阴影部分的面积是
如图，菱形ABCD的边长为2，BD=2，E、F分别是边AD，CD上的两个动点，且满足AE+CF=2．
25、菱形ABCD的边长为24厘米，∠A=60°，质点P从点A出发沿着AB-BD-DA作匀速运动，质点Q从点D同时出发沿着线路DC-CB-BD作匀速运动．
面积．