题目内容
18.已知$\sqrt{a-1}$+(ab-2)2=0.求$\frac{1}{ab}+\frac{1}{{({a+1})({b+1})}}+\frac{1}{{({a+2})({b+2})}}+…+\frac{1}{{({a+2014})({b+2014})}}$的值.
分析 先根据非负数的性质求出a、b的值,再代入代数式进行计算即可.
解答 解:∵$\sqrt{a-1}$+(ab-2)2=0,
∴a-1=0,ab-2=0,解得a=1,b=2,
∴原式=$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2015×2016}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2015}$-$\frac{1}{2016}$
=1-$\frac{1}{2016}$
=$\frac{2015}{2016}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
7.下列各点在正比例函数y=-2x的图象上的点是( )
| A. | (1,2) | B. | (-1,2) | C. | (0.5,1) | D. | (-2,1) |
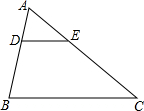 如图,在△ABC中,DE∥BC,AD=2,DB=4,DE=3,则BC的长为9.
如图,在△ABC中,DE∥BC,AD=2,DB=4,DE=3,则BC的长为9.



