题目内容
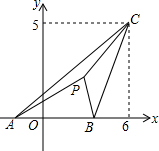 如图所示,已知在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-2,0),B(4,0),C(6,5).在△ABC内存在一点P,使得△ACP的面积与△BCP的面积相等,则直线CP的函数解析式为
如图所示,已知在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-2,0),B(4,0),C(6,5).在△ABC内存在一点P,使得△ACP的面积与△BCP的面积相等,则直线CP的函数解析式为考点:一次函数综合题
专题:
分析:根据等底三角形的面积相等,可得三角形的高相等,根据全等三角形的判定与性质,可得AG与BG的关系,根据待定系数法,可得函数解析式.
解答:解:如图,
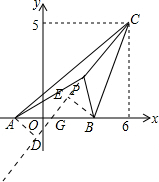
延长CP交x轴与G点,过A点作AD⊥CP与D点,过B点作BE⊥CP与E点,
∴S△ACP=
CP•AD,S△BCP=
CP•BE.
∵S△ACP=S△BCP,
∴AD=BE.
在△ADG和△BEG中,
,
∴△ADG≌△BEG(AAS),
∴AG=BG,
即G点是线段AB的中点,
∵A(-2,0),B(4,0),
∴G点坐标是(1,0).
即使得△ACP的面积与△BCP的面积相等的直线CP经过G点.
设直线CP的函数解析式为y=kx+b,
将C、G点的坐标分别代入函数解析式,得
.
解得
.
直线CP的函数解析式为y=x-1,
故答案为:y=x-1.

延长CP交x轴与G点,过A点作AD⊥CP与D点,过B点作BE⊥CP与E点,
∴S△ACP=
| 1 |
| 2 |
| 1 |
| 2 |
∵S△ACP=S△BCP,
∴AD=BE.
在△ADG和△BEG中,
|
∴△ADG≌△BEG(AAS),
∴AG=BG,
即G点是线段AB的中点,
∵A(-2,0),B(4,0),
∴G点坐标是(1,0).
即使得△ACP的面积与△BCP的面积相等的直线CP经过G点.
设直线CP的函数解析式为y=kx+b,
将C、G点的坐标分别代入函数解析式,得
|
解得
|
直线CP的函数解析式为y=x-1,
故答案为:y=x-1.
点评:本题考查了一次函数综合题,利用了等底等面积的三角形的关系,全等三角形的判定与性质,待定系数法求解析式.

练习册系列答案
相关题目
估算
-3的值是( )
| 101 |
| A、在5与6之间 |
| B、在6与7之间 |
| C、在7与8之间 |
| D、在8与9之间 |
 如图,已知点C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形面积,S2表示长为AB、宽为AC的矩形面积,则S1与S2的大小关系为( )
如图,已知点C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形面积,S2表示长为AB、宽为AC的矩形面积,则S1与S2的大小关系为( )| A、S1>S2 |
| B、S1=S2 |
| C、S1<S2 |
| D、不能确定 |
下列各组数中,互为相反数的是( )
A、
| ||
| B、3与-(-3) | ||
| C、52与-25 | ||
| D、-2与|-2| |

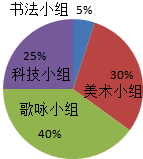 观察统计图,回答问题:
观察统计图,回答问题: