题目内容
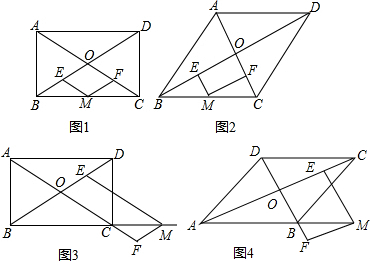
15.阅读材料:如图1,四边形ABCD的对角线AC、BD交于点O,点M是AB边上的一点,过点M分别作ME∥BD,MF∥AC交直线AC、BD于点E、F,显然四边形OEMF是平行四边形.探究发现:
(1)当对角线AC,BD满足AD⊥BD时,四边形OEMF是矩形.
(2)如图2,若四边形ABCD是菱形,且M是AB的中点,判断四边形OEMF是什么特殊的平行四边形,并写出证明过程.
拓展延伸:
(3)如图3,在四边形ABCD为矩形的条件下,若点M是边AB延长线上的一点,此时OA,ME,MF三条线段之间存在怎样的数量关系?并说明理由.
(4)如图4,若四边形ABCD为菱形,且AC:BD=k,请直接写出OA、ME、MF三条线段之间的数量关系(不需要证明).
分析 (1)根据平行四边形的判定证得四边形OEMF是平行四边形,由AD⊥BD,由矩形的判定可证得结论;
(2)首先证得四边形OEMF是平行四边形,然后利用菱形的对角线互相垂直证得∠EOF=90°,利用有一个角是直角的平行四边形是矩形证得结论;
(3)根据四边形OEMF是平行四边形,得到OE=MF,根据四边形ABCD是矩形,得到OB=$\frac{1}{2}$BD,OC=$\frac{1}{2}$AD,且AC=BD,从而得到OB=OC,进一步得到BE=ME,从而证得结论OB=BE-OE=ME-MF;
(4)由相似三角形的判定证得△AOB∽△MFB,根据相似三角形的性质可证得$\frac{AO}{BO}=\frac{MF}{BF}$,于是得到AO=kBO,MF=kBF,代入即可得到结论.
解答 解:(1)当AD⊥BD时,四边形OEMF是矩形,
理由:∵ME∥BD,MF∥AC,
∴四边形OEMF是平行四边形,
∵AD⊥BD,
∴四边形OEMF是矩形,
故答案为:AD⊥BD;
(2)是矩形,
理由:∵ME∥AC,MF∥BD,
∴四边形OEMF是平行四边形.
又∵四边形ABCD是菱形,
∴AC⊥BD,即∠EOF=90°,
∴四边形OEMF是矩形;
(3)结论:OB=ME-MF.
理由如下:∵ME∥AC,MF∥BD,
∴四边形OEMF 是平行四边形,
∴OE=MF,
又∵四边形ABCD是矩形,
∴OB=$\frac{1}{2}$BD,OC=$\frac{1}{2}$AD,且AC=BD,
∴OB=OC,
∴∠OBC=∠OCB,
由ME∥AC可知,∠OCB=∠EMB,
∴BE=ME,
∴OB=BE-OE=ME-MF;
(4)OA+MF=kME,
理由:∵四边形ABCD为菱形,
∴AC=2AO,BD=2BO,
由(2)知,四边形OEMF是矩形,
∴∠EOB=∠F=90°,ME=OF,
∵∠ABO=∠MBF,
∴△AOB∽△MFB,
∴$\frac{AO}{MF}=\frac{BO}{BF}$,
∴$\frac{AO}{BO}=\frac{MF}{BF}$,
AC:BD=k,
∴$\frac{AO}{BO}$=k,
∴$\frac{MF}{BF}$=k,
∴MF=kBF,
∵kME=k(OB+BF)=kOB+kBF=AO+MF,
即OA+MF=kME.
点评 本题考查了矩形的性质及判断、菱形的性质、平行四边形的性质及判定,相似三角形的判定和性质,涉及的知识点比较多,解本题的关键是熟练特殊四边形的性质和判定,本题的疑点是特殊四边形的性质和判定的区别.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案| A. | 某校初二年级共有480人,则至少有两人的生日是同一天 | |
| B. | 经过路口,恰好遇到红灯 | |
| C. | 打开电视,正在播放动画片 | |
| D. | 抛一枚硬币,正面朝上 |
| A. | -3ab2 | B. | -3ab | C. | 3ab | D. | 3ab2 |
| A. | 0是最小的整数 | B. | 0的倒数是0 | ||
| C. | 0是正数也是有理数 | D. | 0是非负数 |
| A. | -12xy3 | B. | 2y3 | C. | 12xy | D. | 2xy3 |
 有理数a,b在数轴上的位置如图,在下列关系中,不成立的是( )
有理数a,b在数轴上的位置如图,在下列关系中,不成立的是( )| A. | a-b>0 | B. | ab>0 | C. | $\frac{1}{a}$>$\frac{1}{b}$ | D. | a+b>a-b |