题目内容
 按图填空,并注明理由.
按图填空,并注明理由.已知:如图,∠1=∠2,∠3=∠E.求证:AD∥BE.
证明:∵∠1=∠2 (已知)
∴
∴∠E=∠
又∵∠E=∠3 ( 已知 )
∴∠3=∠
∴AD∥BE.
考点:平行线的判定与性质
专题:推理填空题
分析:首先根据∠1=∠2可得BD∥CE,再根据平行线的性质可得∠E=∠4,然后可证出∠3=∠4,再根据内错角相等,两直线平行可得AD∥BE.
解答:证明:∵∠1=∠2 (已知),
∴BD∥CE( 内错角相等,两直线平行 ),
∴∠E=∠4(两直线平行,内错角相等 ),
又∵∠E=∠3 (已知 ),
∴∠3=∠4(等量代换),
∴AD∥BE.
∴BD∥CE( 内错角相等,两直线平行 ),
∴∠E=∠4(两直线平行,内错角相等 ),
又∵∠E=∠3 (已知 ),
∴∠3=∠4(等量代换),
∴AD∥BE.
点评:此题主要考查了平行线的判定和性质,关键是掌握内错角相等,两直线平行.两直线平行,内错角相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列式子:x2+2,
,
,0,
,-4y中,整式的个数是( )
| 1 |
| a |
| 3ab |
| 5 |
| ab |
| c |
| A、3 | B、4 | C、5 | D、6 |
 如图,在四边形ABCD中,AB∥CD,∠A=110°,∠ABC=∠ADC,BE平分∠ABC,与CD相交于点E,DF平分∠ADC,与AB相交于点F.
如图,在四边形ABCD中,AB∥CD,∠A=110°,∠ABC=∠ADC,BE平分∠ABC,与CD相交于点E,DF平分∠ADC,与AB相交于点F. 如图,长方形ABCD的边AB=CD=4,AD=BC=2,点E为CD的中点,连接AE、BE,求△AEB的周长.
如图,长方形ABCD的边AB=CD=4,AD=BC=2,点E为CD的中点,连接AE、BE,求△AEB的周长. 如图是由八个相同小正方体组合而成的几何体,从正面、左面、上面观察这个几何体,请分别画出你所看到的几何体的形状图.
如图是由八个相同小正方体组合而成的几何体,从正面、左面、上面观察这个几何体,请分别画出你所看到的几何体的形状图.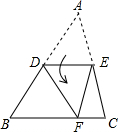 如图,点D、E分别为边AB、AC的中点,将△ABC沿线段DE折叠,使点A落在点F处,若∠B=50°,则∠BDF=
如图,点D、E分别为边AB、AC的中点,将△ABC沿线段DE折叠,使点A落在点F处,若∠B=50°,则∠BDF=