题目内容
7.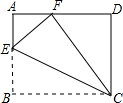 如图,点E是矩形ABCD的边AB上一点,将△BEC沿CE折叠,使点B落在AD边上的点F处,若△AEF∽△FEC∽△DFC,AB=4,则BC的长是$\frac{8\sqrt{3}}{3}$.
如图,点E是矩形ABCD的边AB上一点,将△BEC沿CE折叠,使点B落在AD边上的点F处,若△AEF∽△FEC∽△DFC,AB=4,则BC的长是$\frac{8\sqrt{3}}{3}$.
分析 由折叠的性质得出△FEC≌△BEC,得出BC=FC,∠BEC=∠FEC,由△AEF∽△FEC∽△DFC,得出∠AEF=∠DFC=∠FEC,求出∠DFC=60°,在Rt△CDF中,运用三角函数sin∠DFC=$\frac{DC}{FC}=\frac{AB}{BC}$,即可得出结果.
解答 解:由折叠的性质得:△FEC≌△BEC,
∴BC=FC,∠BEC=∠FEC,
∵四边形ABCD是矩形,
∴DC=AB,
∵△AEF∽△FEC∽△DFC,
∴∠AEF=∠DFC=∠FEC,
∴∠AEF=∠FEC=∠BEC,
∴∠DFC=60°,
在Rt△CDF中,sin∠DFC=$\frac{DC}{FC}=\frac{AB}{BC}$=$\frac{\sqrt{3}}{2}$;
∵AB=4,
∴BC=$\frac{8\sqrt{3}}{3}$,
故答案为:$\frac{8\sqrt{3}}{3}$
点评 本题考查了翻折变换的性质、矩形的性质、相似三角形的性质、三角函数;熟练掌握矩形的性质、折叠的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
2.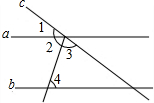 如图,直线a,b被直线c所截,a∥b,若∠2=∠3,∠4=63°,则∠1等于( )
如图,直线a,b被直线c所截,a∥b,若∠2=∠3,∠4=63°,则∠1等于( )
 如图,直线a,b被直线c所截,a∥b,若∠2=∠3,∠4=63°,则∠1等于( )
如图,直线a,b被直线c所截,a∥b,若∠2=∠3,∠4=63°,则∠1等于( )| A. | 54° | B. | 58° | C. | 63° | D. | 68° |
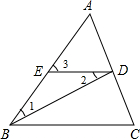 如图,BD平分∠ABC,ED∥BC,∠1=28°.求∠2、∠3的度数.
如图,BD平分∠ABC,ED∥BC,∠1=28°.求∠2、∠3的度数.