题目内容
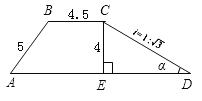
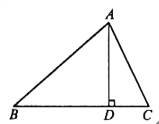
【题目】如图,在△ABC中,AD是BC边上的高, ![]() .
.
(1)求证:AC=BD;
(2)若![]() ,直接写出AD的长是__________.
,直接写出AD的长是__________.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:
(1)由AD是△ABC中BC边上的高,可得∠ADB=∠ADC=90°,结合tanB=cos∠DAC可得![]() 即可得到AC=BD;
即可得到AC=BD;
(2)由sinC=![]() ,若设AD=12x,则AC=13x,由(1)中结论AC=BD可得BD=13x,在Rt△ADC中可得CD=5x,即可得到BC=BD+CD=18x=34,由此可得x=
,若设AD=12x,则AC=13x,由(1)中结论AC=BD可得BD=13x,在Rt△ADC中可得CD=5x,即可得到BC=BD+CD=18x=34,由此可得x=![]() ,则AD=12x=
,则AD=12x=![]() .
.
试题解析:
(1)∵AD是△ABC中BC边上的高,
∴∠ADB=∠ADC=90°,
∴tanB=![]() ,cos∠DAC=
,cos∠DAC=![]() ,
,
又∵tanB=cos∠DAC,
∴![]() ,
,
∴AC=BD;
(2)∵sinC=![]() ,
,
∴若设AD=12x,则AC=13x,
∴在Rt△ADC中,CD=5x,
∵AC=BD,
∴BD=13x,
∴BC=BD+CD=18x,
又∵BC=34,
∴18x=34,解得:x=![]() ,
,
∴AD=12x=![]() .
.

练习册系列答案
相关题目