题目内容
4. 已知:如图,点E,F在AC上,AD∥CB,且AD=CB,∠1=∠2,BD与EF相交于点O,求证:OE=OF.
已知:如图,点E,F在AC上,AD∥CB,且AD=CB,∠1=∠2,BD与EF相交于点O,求证:OE=OF.
分析 根据两直线平行,内错角相等可得∠A=∠C,然后利用“角角边”证明△AOD和△COB全等,根据全等三角形对应边相等可得AO=CO,利用“角边角”证明△ADF和△CBE全等,根据全等三角形对应边相等可得AF=CE,然后相减即可得证.
解答 证明:∵AD∥CB,
∴∠A=∠C,
在△AOD和△COB中,$\left\{\begin{array}{l}{∠A=∠C}\\{∠AOD=∠COB}\\{AD=CB}\end{array}\right.$,
∴△AOD≌△COB(AAS),
∴AO=CO,
在△ADF和△CBE中,$\left\{\begin{array}{l}{∠A=∠C}\\{AD=CB}\\{∠1=∠2}\end{array}\right.$,
∴△ADF≌△CBE(ASA),
∴AF=CE,
∴CO-CE=AO-AF,
即OE=OF.
点评 本题考查了全等三角形的判定与性质,平行线的性质,熟练掌握三角形全等的判定方法是解题的关键,难点在于二次证明三角形全等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.关于$\sqrt{18}$的叙述错误的是( )
| A. | 它是一个无限不循环小数 | B. | 它在3和4之间 | ||
| C. | 它化简后为3$\sqrt{2}$ | D. | 以它为直径的圆的面积是$\frac{9}{2}$π |
15.一组数据0,1,5,2,5,3,3,10的中位数是( )
| A. | 2.5 | B. | 3.5 | C. | 3 | D. | 5 |
19.在下列的四个几何体中,其主视图与俯视图相同的是( )
| A. |  圆柱 | B. |  圆锥 | C. |  三棱柱 | D. |  球 |
9.下列有关使用大雁DY-570学生计算器的说法错误的是( )
| A. | 求5.2×10-2的按键顺序是 | |
| B. | 求($\frac{\sqrt{3}}{3}$)2的按键顺序是 | |
| C. | 求π×103的值的按键顺序是 | |
| D. | 求($\frac{1}{2}$)3的按键顺序是 |
 某校男子足球队的年龄分布如图的条形图,请求出这些队员年龄的平均数、中位数15,15.
某校男子足球队的年龄分布如图的条形图,请求出这些队员年龄的平均数、中位数15,15.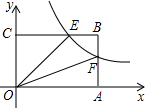 如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OABC的边AB,BC的点F,E,若$\frac{CE}{BE}$=$\frac{3}{2}$且四边形OEBF的面积为4,则该反比例函数解析式是y=$\frac{6}{x}$.
如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OABC的边AB,BC的点F,E,若$\frac{CE}{BE}$=$\frac{3}{2}$且四边形OEBF的面积为4,则该反比例函数解析式是y=$\frac{6}{x}$. 如图所示,在△ABC中,AB:BC:CA=3:4:5且周长为36cm,点P从点A开始沿AB边向B点以每秒2cm的速度移动,点Q从点C沿CB边向点B以每秒1cm的速度移动,如果同时出发,则过3秒时,求△BPQ的面积.
如图所示,在△ABC中,AB:BC:CA=3:4:5且周长为36cm,点P从点A开始沿AB边向B点以每秒2cm的速度移动,点Q从点C沿CB边向点B以每秒1cm的速度移动,如果同时出发,则过3秒时,求△BPQ的面积.