题目内容
15.为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1视为一个整体,设x2-1=y,则y2=(x2-1)2,原方程可化为y2-5y+4=0,解此方程,得y1=1,y2=4.当y=1时,x2-l=l,x2=2,∴x=±$\sqrt{2}$.
当y=4时,x2-l=4,x2=5,∴x=±$\sqrt{5}$
∴原方程的解为x1=-$\sqrt{2}$,x2=$\sqrt{2}$,x3=-$\sqrt{5}$,x4=$\sqrt{5}$.
以上方法就叫换元法,达到了降次的目的,体现了转化的思想.运用上述方法解下列方程:
(1)x4-3x2-4=0;
(2)(x2+x)(x2+x-2)=-1.
分析 (1)设t=x2,则原方程转化为关于t的一元二次方程t2-3t-4=0,通过解该方程得到t的值,然后解关于x的一元二次方程即可;
(2)设y=x2+x,则原方程转化为关于y的一元二次方程y(y-2)=-1,通过解方程求得y的值,然后解关于x的一元二次方程.
解答 解:(1)设t=x2,则t2-3t-4=0,
所以:(t-4)(t+1)=0,
解得t=4或t=-1(舍去).
则x2=4,
解得x=-2,x=2.
因此方程的根为x1=2,x2=-2;
(2)设y=x2+x,则y(y-2)=-1,
所以(y-1)2=0,
解得y1=y2=1,
所以x2+x=1.即x2+x-1=0.
则x=$\frac{-1±\sqrt{5}}{2}$,
解得,x1=$\frac{-1+\sqrt{5}}{2}$,x2=$\frac{-1-\sqrt{5}}{2}$.
点评 本题主要考查了换元法,即把某个式子看作一个整体,用一个字母去代替它,实行等量替换.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.下列等式从左到右的变形是因式分解的是( )
| A. | 6a3b=3a2•2ab | B. | (x+2)(x-2)=x2-4 | ||
| C. | 2x2+4x-3=2x(x+2)-3 | D. | ax-ay=a(x-y) |
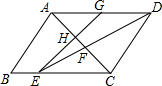 如图,已知?ABCD,DE平分∠ADC分别交BC、AC于点E、F,G是AD中点,EG交AC于点H.若AB=4,AD=6.求
如图,已知?ABCD,DE平分∠ADC分别交BC、AC于点E、F,G是AD中点,EG交AC于点H.若AB=4,AD=6.求 如图,在四边形ABCD中,已知∠A=100°,∠D=90°,∠E=120°,∠3=40°,则∠1+∠2=60°,∠4=70°.
如图,在四边形ABCD中,已知∠A=100°,∠D=90°,∠E=120°,∠3=40°,则∠1+∠2=60°,∠4=70°.