题目内容
一元二次方程ax2+bx+c=0（a＜0）的两个实数根分别为x1、x2，x1=-2、1＜x2＜2，则
- A.a＜b＜0
- B.0＜a＜b
- C.b＜a＜0
- D.0＜b＜a
A
分析：利用一元二次方程的根与系数的关系求得x2-2=-
②；然后不等式的性质解答1＞＞0，知0＜b＜a．
解答：∵元二次方程ax2+bx+c=0（a＜0）的两个实数根分别为x1、x2，x1=-2，
∴x2-2=-，②
又∵1＜x2＜2，
∴-1＜x2-2＜0，即1＞＞0，
而a＜0，
∴a＜b＜0．
故选A．
点评：此题主要考查了根与系数的关系，将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法．
分析：利用一元二次方程的根与系数的关系求得x2-2=-
②；然后不等式的性质解答1＞＞0，知0＜b＜a．解答：∵元二次方程ax2+bx+c=0（a＜0）的两个实数根分别为x1、x2，x1=-2，
∴x2-2=-
，②又∵1＜x2＜2，
∴-1＜x2-2＜0，即1＞
＞0，而a＜0，
∴a＜b＜0．
故选A．
点评：此题主要考查了根与系数的关系，将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法．
练习册系列答案
相关题目
一元二次方程ax2+bx+c=0（a≠0，b2-4ac≥0）的两实根之和（ ）
| A、与c无关 | B、与b无关 | C、与a无关 | D、与a，b，c都有关 |
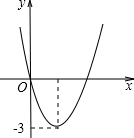（2012•泰安）二次函数y=ax2+bx的图象如图，若一元二次方程ax2+bx+m=0有实数根，则m的最大值为（ ）