题目内容
17. 如图所示,一块直角三角板ABC,∠ACB=90°,将直角三角板绕着顶点B顺时针旋转60°使得点C旋转到AB边上的一点D,点A旋转到点E的位置,点F、G分别是BD、BE上的点,BF=BG,延长CF与DG交于点H.
如图所示,一块直角三角板ABC,∠ACB=90°,将直角三角板绕着顶点B顺时针旋转60°使得点C旋转到AB边上的一点D,点A旋转到点E的位置,点F、G分别是BD、BE上的点,BF=BG,延长CF与DG交于点H.(1)求证:CF=DG;
(2)判断△ABE的形状;
(3)求出∠FHG的度数.
分析 (1)在△CBF和△DBG中,利用SAS即可证得两个三角形全等,利用全等三角形的对应边相等即可证得;
(2)由旋转直接∠ABE=60°,BA=BE,从而得出△ABE是等边三角形;
(3)根据全等三角形的对应角相等,以及三角形的内角和定理,即可证得∠DHF=∠CBF=60°,从而求解
解答 (1)证明:∵在△CBF和△DBG中,$\left\{\begin{array}{l}{BC=BD}\\{∠CBF=∠DBG}\\{BF=BG}\end{array}\right.$,
∴△CBF≌△DBG(SAS),
∴CF=DG;
(2)△ABE是等边三角形,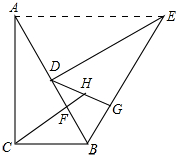
理由:如图,连接AE,
∵直角三角板ABC绕着顶点B顺时针旋转60°使得点C旋转到AB边上的一点D,点A旋转到点E的位置,
∴∠ABE=60°,BA=BE,
∴△ABE是等边三角形;
(3)解:由(1)△CBF≌△DBG,
∴∠BCF=∠BDG,
又∵∠CFB=∠DFH,
又∵△BCF中,∠CBF=180°-∠BCF-∠CFB,
△DHF中,∠DHF=180°-∠BDG-∠DFH,
∴∠DHF=∠CBF=60°,
∴∠FHG=180°-∠DHF=180°-60°=120°
点评 此题是几何变换综合题,主要考查了旋转的性质,全等三角形的判定和性质,等边三角形的判定,三角形的内角和,解本题的关键是判断出△CBF≌△DBG.

练习册系列答案
相关题目
5.下列语句中正确的是( )
| A. | 同一平面内,不相交的两条直线叫做平行线 | |
| B. | 过一点有且只有一条直线与已知直线平行 | |
| C. | 两直线平行,同旁内角相等 | |
| D. | 两条直线被第三条直线所截,同位角相等 |
2.如图所示,将一个圆依次二等分、三等分、四等分、五等分…,并按图中规律在半径上摆放棋子,图1中有5个棋子,图2中有10个棋子,图3中有17个棋子…,以此规律,图6中所含棋子数为( )


| A. | 51 | B. | 50 | C. | 49 | D. | 48 |
9.半径为1的圆中有一条弦,如果它的长为$\sqrt{3}$,那么这条弦所对的圆周角为( )
| A. | 60° | B. | 120° | C. | 45° | D. | 60°或120° |
17.“比a的3倍大5的数”用代数式表示为( )
| A. | 3a+5 | B. | 3(a+5) | C. | 3a-5 | D. | 3(a-5) |

 如图,在平面直角坐标系中,直线y=kx与抛物线y=ax2+c交于A(8,6)、B两点,点B的横坐标为-2.
如图,在平面直角坐标系中,直线y=kx与抛物线y=ax2+c交于A(8,6)、B两点,点B的横坐标为-2. 已知:如图,在Rt△ABC中,∠B=30°,∠C=90°,BD=AD,BD=12
已知:如图,在Rt△ABC中,∠B=30°,∠C=90°,BD=AD,BD=12