题目内容
如图1－81所示，A，B是公路l（l为东西走向）两旁的两个村庄，A村到公路l的距离AC＝1 km，B村到公路l的距离BD＝2 km，B村在A村的南偏东45°方向上．
（1）求A，B两村之间的距离；
（2）为方便村民出行，计划在公路边新建一个公共汽车站P，要求该站到两村的距离相等，请用尺规在图中作出点P的位置．（保
留清晰的作图痕迹，并简要写明作法）
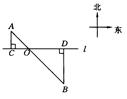
解：如图1－83所示．（1）方法1：设AB与CD的交点为O，根据题意可得∠A=∠OBD=45°，∴△ACO和△BDO都是等腰直角三角形，∴AO＝
，BO＝
，∴A，B两村的距离为AB=AO＋BO＝＋2＝3 （km）．方法2：过点B作直线l的平行线交AC的延长线于E，易证四边形CDBE是矩形，∴C
E＝BD＝2．在Rt△AEB中，由∠A=45°，可得EF＝CA＝3，∴AB＝
（km）．
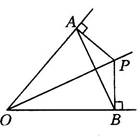
（2）作法：①分别以点A，B为圆心，以大于
AB的长为半径作弧，两弧交于两点M，N，作直线MN；②直线MN交l于点P，点P即为所求．
练习册系列答案
相关题目
则∠Ａ＝＿＿＿＿。
分 成了两个等腰三角形，
那么α的度数为 ．
划分方案．牧童B的划分方案如图1－49（2）所示，三块矩形的面积相等，牧童的位置在三个小矩形的中心．牧童C的划分方案如图1－49（3）所示，把正方形的牧场分成三块矩形，牧童的位置在三个小矩形的中心，并保证在有情况时三个要所需走的最大距离相等．
，B=
，问：A与B哪个大？