题目内容
6. 有理数a、b、c在数轴上的位置如图所示,且表示数a的点与表示数b的点到原点的距离相等
有理数a、b、c在数轴上的位置如图所示,且表示数a的点与表示数b的点到原点的距离相等(1)计算a+b-$\frac{3c}{b}$;
(2)确定a+c,b+c,a-c,b-c的符号;
(3)求|a+c|+|2b|+|a-c|+|3c|的值.
分析 (1)根据表示数a的点与表示数b的点到原点距离相等可以得到a、b互为相反数,据此即可求解;
(2)根据数轴上右边的数总是大于左边的数和有理数的加法法则即可作出判断;
(3)先判断a+c,2b,a-c,3c的符号,再去掉绝对值符号,计算即可.
解答 解:(1)∵表示数a的点与表示数b的点到原点距离相等,
∴a+b=0,
则原式=(a+b)-$\frac{3c}{b}$=0-$\frac{3c}{b}=-\frac{3c}{b}$;
(2)根据数轴可知:b<c<0<a;|a|=|b|>|c|;
则a+c>0,b+c<0,a-c>0,b-c<0;
(3)∵a+c>0,2b<0,a-c>0,3c<0,
∴原式=a+c-2b+a-c-3c=2a-2b-3c.
点评 本题考查了数轴与有理数大小的比较,理解a、b互为相反数是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.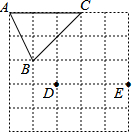 如图是5×5的正方形网格中,以D、E为顶点作位置不同的格点的三角形与△ABC全等,这样格点三角形最多可以画出( )
如图是5×5的正方形网格中,以D、E为顶点作位置不同的格点的三角形与△ABC全等,这样格点三角形最多可以画出( )
 如图是5×5的正方形网格中,以D、E为顶点作位置不同的格点的三角形与△ABC全等,这样格点三角形最多可以画出( )
如图是5×5的正方形网格中,以D、E为顶点作位置不同的格点的三角形与△ABC全等,这样格点三角形最多可以画出( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
11.已知A=5a-3b,B=-6a+4b,则A-B等于( )
| A. | -a+b | B. | 11a+b | C. | 11a-7b | D. | -a-7b |