题目内容
【题目】已知:在矩形![]() 中,
中,![]() ,
,![]() ,四边形
,四边形![]() 的三个顶点
的三个顶点![]() 、
、![]() 、
、![]() 分别在矩形
分别在矩形![]() 边
边![]() 、
、![]() 、
、![]() 上,
上,![]() .
.
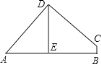
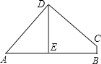
![]() 如图
如图![]() ,当四边形
,当四边形![]() 为正方形时,求
为正方形时,求![]() 的面积;
的面积;
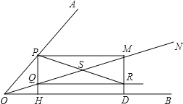
![]() 如图
如图![]() ,当四边形
,当四边形![]() 为菱形时,设
为菱形时,设![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出函数的定义域.
的函数关系式,并写出函数的定义域.

【答案】(1)10;(2)![]() ,(
,(![]() ).
).
【解析】
(1)只要证明△AEH≌△BFE.推出BF=AE=2,由△MGF≌△BFE,推出△MGF≌△AEH,求出FC、GM即可解决问题;
(2)过点G作GM⊥BC,垂足为M,连接HF,根据S△GFC=![]() FCGM,计算即可.
FCGM,计算即可.
(1)如图![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,

由矩形![]() 可知:
可知:![]() ,
,
由正方形![]() 可知:
可知:
![]() ,
,![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
同理可证:![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() .
.
![]() 如图
如图![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.

由矩形![]() 得:
得:![]() ,
,
∴![]() ,
,
由菱形![]() 得:
得:![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
∴![]() ,
,
即:![]() ,
,
定义域:![]() .
.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目